Línea de transmisión larga

Una línea de transmisión con una longitud superior a 240 km se considera como línea de transmisión larga. En una línea de transmisión larga, los parámetros se distribuyen uniformemente a lo largo de toda la línea. Para una línea de transmisión larga, se considera que la línea se puede dividir en varias secciones, y cada sección consta de una inductancia, capacitancia, resistencia y conductancia, como se muestra a continuación.

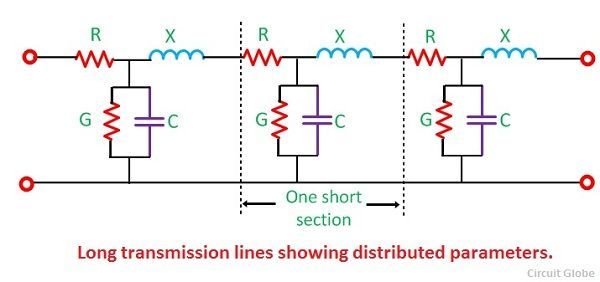Consideremos una parte un poco más pequeña de una línea de transmisión larga que tiene una longitud ‘ds’ situada a una distancia ‘s’ del extremo receptor. La impedancia en serie de la línea está representada por ‘zds’ y ‘yds’ es la impedancia en derivación de la línea. Debido a la corriente de carga y la pérdida de corona, la corriente no es uniforme a lo largo de la línea. El voltaje también es diferente en diferentes partes de la línea debido a la reactancia inductiva.

Donde, r – resistencia por unidad de longitud, por fase
l – inductancia por unidad de longitud, por fase
c – capacitancia por unidad de longitud, por fase
x – reactancia inductiva por unidad de longitud, por fase
z – impedancia en serie por unidad de longitud, por fase
g – conductancia de fuga de derivación, por fase a neutro por unidad de longitud
b – susceptibilidad de fuga de derivación, por fase a neutro por unidad de longitud
y – admitancia de derivación por unidad de longitud, por fase a neutro.

Para suministro constante sea,

V – voltaje a una distancia ‘s’ del extremo de la carga
V + dV: tensión a una distancia (s+ds) del extremo de la carga
I – corriente a una distancia ‘s’ del extremo de la carga
I + dI: corriente a una distancia (s+ds) del extremo de la carga.

La diferencia de voltaje entre los extremos de las secciones supuestas de longitud ds es dV. Esta diferencia es causada por la impedancia en serie de la línea.

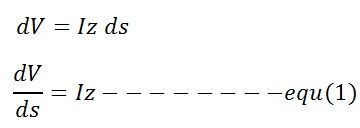Análogamente, la diferencia entre los dos extremos de la sección resultante de la admitancia en derivación de la línea viene dada por la ecuación

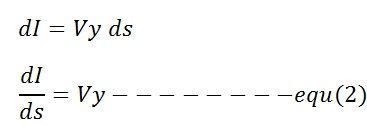para conocer el valor de V, diferencie la ecuación (1) con respecto a ‘s’,

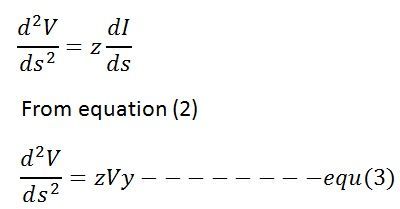y para diferenciar la ecuación actual (2)

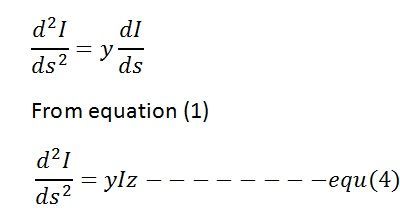las ecuaciones (3) y (4) son similares en forma y, por lo tanto, sus ecuaciones generales también son similares.

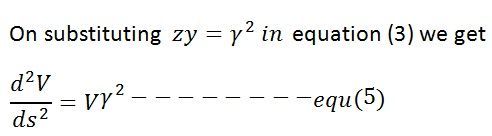La ecuación (5) es la ecuación diferencial lineal con coeficientes constantes. La solución general de esta ecuación es

Donde, C1 y C2 son las constantes arbitrarias, y se encuentra a partir del valor conocido de V e I en algún punto de la recta. Para determinar el valor de diferencio la ecuación anterior con respecto a ‘s’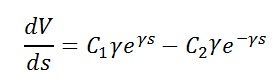 al combinar la ecuación anterior con la ecuación (1) obtenemos,

sustituyendo el valor de ϒ = √zy en la ecuación (7) da

El valor de V e I en el extremo receptor, donde s = 0, viene dado por las ecuaciones

Los valores de C1 y C2 se encuentran a partir de las ecuaciones simultáneas que se muestran a continuación.

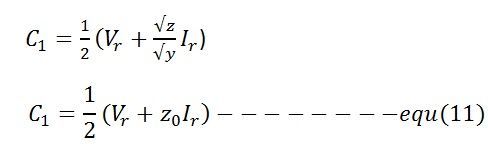y

Los valores de C1 y C2 se sustituyen en las ecuaciones generales de voltaje y corriente para obtener los valores de estado estacionario de V e I en cualquier punto intermedio distante ‘s’ del extremo receptor.

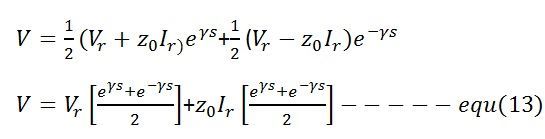y

Para gobernar el comportamiento de la línea de transmisión en estado estacionario se utilizan las ecuaciones (13) y (14). Estas ecuaciones también se pueden escribir en forma hiperbólica usando la constante hiperbólica que se muestra a continuación

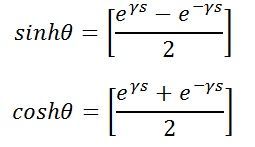Sustituye la constante hiperbólica en las ecuaciones (13) y (14) da

estas ecuaciones también se pueden escribir como ecuaciones de corriente y voltaje final de envío reemplazando s = S

Los parámetros ABCD se definen a continuación

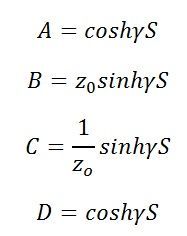Estas ecuaciones ayudan a evaluar el rendimiento del palangre.

Publicaciones relacionadas:

¿Qué es la ondulación y el factor de ondulación? – Fórmula del factor de ondulación Línea de transmisión de circuito simple y circuito doble Diferencia entre amplificador inversor y no inversor ¿Cuál es la clase de aislamiento del aceite de transformador? Conductor electrico Motor síncrono de reluctancia versus motor síncrono de imán permanente Compensador de VAR Estático Diferencia entre fotodiodo y fototransistor Cálculo del factor de multiplicación de medidores de energía Diferencia entre colorímetro y espectrofotómetro Diferencia entre fusible y disyuntor Libros de ingeniería eléctrica: una lista completa