Método iterativo

los Método iterativo es una forma matemática de resolver un problema que genera una secuencia de aproximaciones. Este método es aplicable tanto para problemas lineales como no lineales con un gran número de variables. La palabra Iterativa o Iteración se refiere a la técnica que resuelve cualquier problema de sistema lineal con aproximaciones sucesivas en cada paso. Hay dos métodos bajo métodos iterativos, uno es un método iterativo estacionario y otro es un método iterativo no estacionario.

Entendamos el método iterativo con la ayuda de un ejemplo.

La ecuación de coordinación para la n-ésima planta es Método iterativo eq 1

Supongamos que la planta tiene las funciones de coste cuadráticas de la forma que se indica a continuación. Método iterativo eq 2

Donde,

αn es la pendiente de la curva de costo de producción incremental.
βn es la intersección de la curva de costo de producción incremental en el eje (IC)n.

De la ecuación (1) obtenemos Método iterativo eq 3

Por lo tanto, la ecuación (1) se puede escribir como se muestra a continuación. Método iterativo eq 4

Recolectando todo el coeficiente de Pn obtenemos la siguiente ecuación que se muestra a continuación. Método iterativo eq 5

Despejando el valor de Pn obtendremos.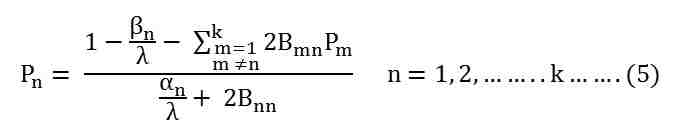 Método iterativo eq 6

La ecuación anterior no se puede resolver directamente. Se resuelve por el método iterativo. El siguiente procedimiento se da a continuación para resolver la ecuación por el método iterativo.

Suponga el valor adecuado de λ = λ0. El costo incremental de las distintas unidades debe ser menor que la intersección del costo incremental de las distintas unidades. Calcule P1, P2 ….. Pn en función de los costos incrementales iguales.
Calcule la generación en todos los buses con la ayuda de la ecuación (5). Los valores de las potencias a sustituir en el lado derecho de la ecuación durante la iteración cero corresponden a los valores calculados en el paso 1.
Verifique si la diferencia entre la potencia en todos los buses del generador y las dos iteraciones consecutivas debe ser menor que un valor especificado. Si no es así, se repite de nuevo el paso 2.
Calcule las pérdidas utilizando la relación que se muestra a continuación.

Método iterativo ecuación 7

Ahora, calcula

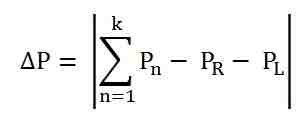
Método iterativo eq 8

Si ΔP es menor que un valor específico ε, detenga el cálculo y calcule el costo de generación con los valores de las potencias. Si ΔP < ε no se cumple, siga el paso que se indica a continuación.
Actualice λ como se muestra a continuación

Método iterativo ecuación 9

Donde, Δλ es el tamaño del paso. El tamaño de paso Δλ se puede seleccionar sobre la base del desajuste de potencia por unidad que se proporciona como se muestra a continuación. Método iterativo eq 10

La conjetura inicial y el tamaño del paso son las dos consideraciones principales en cualquier solución iterativa, ya que la convergencia y el número de iteraciones dependen de estos dos factores. Dado que las pérdidas de transmisión son del 10 al 15 por ciento de la generación total, las pérdidas pueden despreciarse para la suposición inicial en la iteración.