<p style=”text-align: justify;”>Los parámetros ABCD son parámetros generalizados de la línea de transmisión. Estos parámetros son bastante útiles para el cálculo y análisis de la línea de transmisión. En cualquier red de cuatro terminales, la tensión y la corriente de entrada se pueden expresar en términos de la tensión y la corriente de salida, siempre que la red sea pasiva, lineal y bilateral. Afortunadamente, una línea de transmisión es una red de cuatro terminales y sobre todo es una red pasiva, lineal y bilateral. Por lo tanto, el voltaje y la corriente de entrada de la línea de transmisión se pueden expresar en términos de voltaje y corriente de salida.
Para una línea de transmisión, es mejor llamar a la tensión y la corriente de entrada como Tensión y corriente finales de envío. Del mismo modo, el voltaje de salida como el voltaje y la corriente del extremo receptor.
Dejar
VR = Tensión final de recepción
Vs = Tensión final de envío
Is = corriente final de envío
IR = corriente final de recepción
Así podemos escribir,
contra = AVR + BIR …………………..(1)
Es = RCV + DIRECCIÓN ……………………(2)
Aquí A, B, C y D son constantes y se conocen como constantes de circuito generalizadas de la línea de transmisión. Los valores de las constantes se pueden calcular fácilmente a partir de las ecuaciones anteriores. Para calcular los valores de los parámetros ABCD, consideraremos dos casos. El signo en negrita en toda la publicación significa forma vectorial de la cantidad.
Caso (1): cuando el extremo receptor está abierto.
Como el extremo receptor está abierto, la corriente de carga a través de la línea será cero. Así IR = 0.
De la ecuación (1).
A = contra / realidad virtual
Observe que la unidad de A no tiene unidades y, por lo tanto, se llama relación de voltaje.
De la ecuación (2),
C = Es / realidad virtual
De la expresión anterior de la constante C, está claro que la unidad de C es Mho. Esta constante se conoce como conductancia de circuito abierto.
Caso (2): cuando el extremo receptor está en cortocircuito.
Como el extremo receptor está en cortocircuito, el voltaje del extremo de carga será cero. Por lo tanto, VR = 0.
De la ecuación (1),
B = contra / infrarrojos
Tenga en cuenta que la unidad de B es la misma que la de la impedancia, es decir, Ohm y se llama resistencia de cortocircuito.
De la ecuación (2),
D = Es / infrarrojos
Por lo tanto, D es una dimensión menos cantidad y se conoce como relación actual.
Para resumir, los parámetros ABCD para una red pasiva, lineal y bilateral de cuatro terminales se dan como
| Parámetros de circuito generalizados | Valor | Unidad |
| Relación de voltaje, A | contra/VR | Unidad menos |
| Resistencia de cortocircuito, B | contra / IR | Ohm |
| Conductancia de circuito abierto, C | es / RV | Mho |
| Relación actual, D | es / RV | Unidad menos |
Índice de contenidos
Características de los parámetros ABCD
Los siguientes son algunos de los puntos importantes sobre los parámetros ABCD, que siempre se deben tener en cuenta:
- Las constantes A, B, C y D suelen ser números complejos y, por lo tanto, un fasor.
- Para un sistema dado,
A = D
y ANUNCIO – antes de Cristo = 1
Determinación de Parámetros ABCD para Línea de Transmisión
Determinaremos el valor de estos parámetros tanto para líneas de Transmisión Cortas como Medianas.
Línea de transmisión corta – Parámetros ABCD
Como sabemos, el efecto de la capacitancia de derivación en la línea de transmisión corta se ignora, por lo tanto, el circuito equivalente para una sola fase para la línea de transmisión corta se puede mostrar a continuación.
De la figura de arriba,
Es = infrarrojos …………………………(3)
y contra = realidad virtual + IRZ …………..(4)
Comparando la ecuación (3) y (4) con la ecuación (1) y (2), obtenemos
A = 1, B = Z, C = 0 y D = 1
Así vemos que, A = D y AD – BC = 1
Línea de Transmisión Media – Parámetros ABCD
Encontraremos los parámetros ABCD para dos modelos de línea de transmisión media, es decir, para el modelo T nominal y el modelo π nominal.
Modelo T nominal
El diagrama de circuito equivalente para el modelo T nominal para una sola fase de la línea de transmisión se muestra en la figura a continuación.
De la figura de arriba,
vs = V1 + esZ/2 (Estos están en fasor de)
Pero V1 = RV + IRZ/2 (Estos están en fasor de)
Otra vez,
ic = Es – infrarrojos
= V1Y donde Y = admitancia de derivación
= Y (realidad virtual + IRZ/2 )
Por lo tanto,
Es = infrarrojos + YVR + YIRZ/2
= YVR + infrarrojos(1 + YZ / 2) ……………………….(5)
Poner el valor de V1 en la expresión de Vs, obtenemos
contra = realidad virtual + IRZ/2 + esZ/2
Poniendo el valor de Is en la expresión anterior, obtenemos
contra = (1 + YZ / 2)realidad virtual + (Z + YZ2 / 4) infrarrojos ……………(6)
Comparando la ecuación (6) con (1), obtenemos
A = 1 + YZ / 2
B = Z + YZ2 / 4 = Z(1 + YZ / 4)
Comparando la ecuación (5) con (2), obtenemos
C = Y
re = 1 + YZ / 2
Por lo tanto, los parámetros ABCD para el modelo T nominal de la línea de transmisión media son
UN = D = 1 + YZ / 2
B = Z(1 + YZ / 4)
C = Y
Modelo π nominal
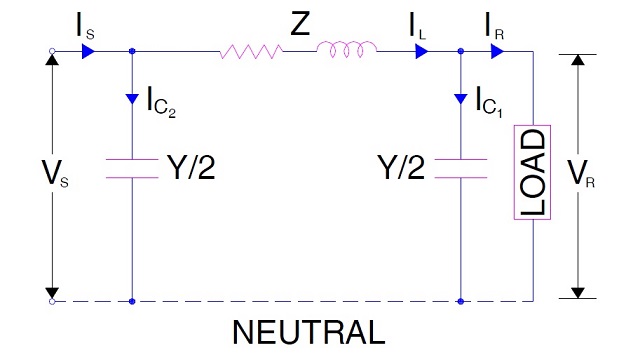
El diagrama de circuito equivalente para el modelo π nominal para una sola fase de la línea de transmisión se muestra en la figura a continuación.
Como se desprende claramente de la figura anterior,
Es = ILLINOIS + IC2
Es = ILLINOIS + vsY/2 donde Y = Admitancia de derivación = jωC
Otra vez,
ILLINOIS = infrarrojos + IC1
= infrarrojos + VRY/2 donde Y = Admitancia de derivación = jωC
Ahora, calcularemos el valor del voltaje y la corriente finales de envío en términos del voltaje y la corriente finales de recepción.
contra = realidad virtual + ILZ
Poniendo el valor de IL, obtenemos
contra = realidad virtual + (infrarrojos + VRY/2) Z
contra = realidad virtual + (infrarrojos + VRY/2) Z
= (1 + YZ/2) realidad virtual + (Z) infrarrojos ………………………………(7)
Ahora,
Es = ILLINOIS + vsY/2
Poner el valor de ILLINOIS obtenemos,
Es = (infrarrojos + VRY/2) + vsY/2
Ahora, poniendo el valor de contra obtenemos,
Es = (infrarrojos + VRY/2) + [(1 + YZ/2) VR + (YZ / 2) IR ]XY/2
= (1+ YZ/2)infrarrojos + Y (1+ YZ/4)realidad virtual ………………………………(8)
Comparando la ecuación (7) con (1),
A = 1 + YZ/2
B = Z
Comparando la ecuación (8) con (2),
C = Y (1+ YZ/4)
re = 1 + YZ/2
Por lo tanto, los parámetros ABCD para el modelo π nominal de la línea de transmisión media son
UN = D = 1 + YZ/2
B = Z
C = Y (1+ YZ/4)
La conformidad de AD – BC = 1 se puede comprobar fácilmente y dejar para el lector. Espero que entiendas este tema con claridad.
Publicaciones relacionadas:
Tipos de contacto de salida de relé 
Desglose de Zener y Desglose de avalancha 
Conexión en estrella en un sistema trifásico 
Filosofía de Protección Primaria y de Respaldo 
diodos 
Diferencia entre contador síncrono y asíncrono 
Maxwell Bridge-Medición de inductancia 
Multiplicador de Voltímetro – Construcción y Cálculo 
¿Por qué el devanado del inducido del generador está conectado en ESTRELLA y no en DELTA? Ventajas del sistema trifásico sobre el monofásico 
Protección de máquina muerta del generador 
Reacción de armadura en alternador o máquina síncrona
