Teorema de Tellegen

Teorema de Tellegen establece que la suma de la potencia entregada es cero para cada ramal de cualquier red eléctrica en cualquier instante de tiempo. Es principalmente aplicable para el diseño de filtros en el procesamiento de señales.

También se utiliza en sistemas operativos complejos para regular la estabilidad. Se utiliza principalmente en el sistema químico y biológico y para encontrar el comportamiento dinámico de la red física.

El teorema de Tellegen es independiente de los elementos de la red. Por lo tanto, es aplicable a cualquier sistema global que tenga elementos lineales, activos, pasivos y variables en el tiempo. Además, el teorema es conveniente para la red que sigue la ley de corriente de Kirchoff y la ley de voltaje de Kirchoff.

Índice de contenidos

Explicación del teorema de Tellegen
Pasos para resolver redes usando el teorema de Tellegen
- Aplicación del teorema de Tellegen

Explicación del teorema de Tellegen

El teorema de Tellegen también se puede expresar con otras palabras, ya que, en cualquier red lineal, no lineal, pasiva, activa, variante en el tiempo o invariable en el tiempo, la suma de la potencia (potencia instantánea o compleja de las fuentes) es cero.

Así, para la rama K-ésima, este teorema establece que:

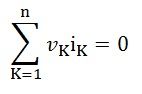
teorema de tellegen eq1

Donde,
n es el número de ramas
vK es el voltaje en la rama

iK es la corriente que circula por la rama.

Dejar,
teorema de tellegen eq2

La ecuación (1) muestra la K-ésima rama a través de la corriente

vK es la caída de voltaje en la rama K y se da como:

Donde vp y vq son los voltajes de nodo respectivos en los nodos p y q.
TEOREMA DE TELLEGEN Tenemos,

También,
teorema de tellegen eq5

Obviamente
teorema de tellegen eq6

Sumando las dos ecuaciones anteriores (2) y (3), obtenemos
teorema de tellegen eq7

Tales ecuaciones se pueden escribir para cada rama de la red.

Suponiendo n ramas, la ecuación será:
teorema de tellegen eq8

Sin embargo, según la ley de corrientes de Kirchhoff (LCK), la suma algebraica de las corrientes en cada nodo es igual a cero.

Por lo tanto,
teorema de tellegen eq9

Así, de la ecuación anterior (4) finalmente, obtenemos
teorema de tellegen eq10

Así, se ha observado que la suma de la potencia entregada a una red cerrada es cero. Esto prueba el teorema de Tellegen y también prueba la conservación de la potencia en cualquier red eléctrica.

También es evidente que la suma de potencia entregada a la red por una fuente independiente es igual a la suma de potencia absorbida por todos los elementos pasivos de la red.

Pasos para resolver redes usando el teorema de Tellegen

A continuación se dan los siguientes pasos para resolver cualquier red eléctrica por el teorema de Tellegen:

Paso 1 – Para justificar este teorema en una red eléctrica, el primer paso es encontrar las caídas de tensión en las ramas.
Paso 2 – Encuentre las corrientes de rama correspondientes utilizando métodos de análisis convencionales.
Paso 3 – Entonces, el teorema de Tellegen se puede justificar sumando los productos de todos los voltajes y corrientes de las ramas.

Por ejemplo, si una red tiene algunas ramas “b” entonces:

teorema de tellegen eq11

Ahora bien, si se toma el conjunto de tensiones y corrientes correspondientes a los dos instantes de tiempo diferentes, t1 y t2, entonces también es aplicable el teorema de Tellegen donde obtenemos la ecuación que se muestra a continuación:

teorema de tellegen eq12

Aplicación del teorema de Tellegen

Las diversas aplicaciones del teorema de Tellegen son las siguientes:

Se utiliza en el sistema de procesamiento de señales digitales para diseñar filtros.
En el área del proceso biológico y químico.
En topología y estructura de análisis de redes de reacción.
El teorema se usa en plantas químicas e industrias petroleras para determinar la estabilidad de cualquier sistema complejo.

Esto es todo sobre el teorema de Tellegen.