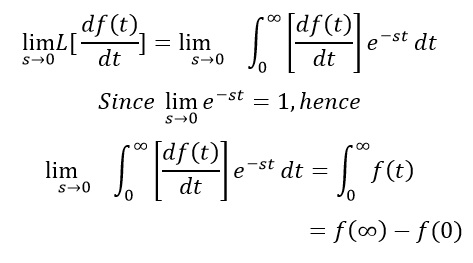El teorema del valor final se utiliza para determinar el valor final de una función de dominio de Laplace F(s). Aunque siempre podemos transformar una función en el dominio del tiempo en Dominio de Laplace para aplicar el teorema del valor final. Según el teorema del valor final, el valor final de una función, es decir, el valor de la función f
Valor final de f
s→0
En una publicación anterior ya hablamos sobre Teorema del valor inicial y muchos puntos importantes que necesitan atención. Discutimos por qué la variable de Laplace s→∞ cuando t→0 para el teorema del valor inicial.
Entonces, en esta publicación no nos centraremos en esos puntos, pero siempre puede consultar la publicación anterior en Teorema del valor inicial refrescar. Procedamos ahora a demostrar este teorema.
Prueba del teorema del valor final:
Como sabemos que L[df
(Puedes pensar por qué tomé el límite (s)→0), ¿por qué no limitar (s→∞). Se sugiere leer el Teorema del Valor Inicial para despejar esta duda. Si aún tiene problemas, escriba en el cuadro de comentarios).
Pero según la definición de Transformación de Laplace,
Por lo tanto,
Así de (1), podemos escribir f(∞) – f(0) = lim [sF(s) – f(0+)]
s→0
Dado que la función existe solo para t≥0, entonces f(0) = f(0+). Además, f(0) es una constante, por lo que se puede sacar del límite. Por eso,
f(∞) – f(0+) = lím sF(s) – f(0+) s→0 ⇒f(∞) = lím sF(s) s→0 Pero f(∞) es el valor de la función cuando t→∞ es decir, valor final, esto significa que el valor final de f
s→0
Solicitud:
Consideremos algunos ejemplos para comprender mejor la aplicación del teorema del valor final.
Ejemplo 1:
Encuentre el valor de estado estacionario de la función dada a continuación
F(s) = 1/s(s+2)(s+5)
Solución:
El valor constante de la función significa el valor final. Por lo tanto, para el ejemplo anterior, calcularemos el valor final.
Ya que, F(s) = 1/s(s+2)(s+5)
Entonces, sF(s) = 1/(s+2)(s+5)
Usando el teorema del valor final,
Valor final = lím sF(s) s→0 = lím [1/(s+2)(s+5)]
s→0 = 1/10 = 0,1 (Respuesta)
Ejemplo-2:
Encuentre la ganancia de estado estacionario y de estado transitorio del circuito de lavado. Un circuito de lavado se define mediante la siguiente función de transferencia.
F(s) = sT / (1+sT) donde T es la constante de tiempo del sistema.
Solución:
La ganancia de estado estacionario se puede encontrar aplicando el Teorema del valor final, mientras que la ganancia de estado transitorio se puede encontrar usando el Teorema del valor inicial.
Ganancia de estado estacionario = lim [sT / (1+sT)]
s→0 = límite [T / (1/s+T)]
s→0 = 0 Ganancia de estado transitorio = lim [sT / (1+sT)]
s→∞ = lím [T / (1/s+T)]
s→∞ = T/ (0+T) = 1
Por lo tanto, la ganancia de estado estable y la ganancia de estado transitorio del circuito de lavado es 0 y 1 respectivamente. Esto significa que el circuito de lavado solo estará activo durante la condición transitoria. No hará nada durante el estado estable del sistema. Tales circuitos son ampliamente utilizados en el sistema de control. Espero que hayas entendido el circuito de lavado también.
Ejemplo-3:
Final, la ganancia en estado estacionario y en estado transitorio de una función escalón unitario.
Solución:
Una función escalón unitario se define mediante la siguiente función de transferencia.
F(s) = 1 / (1+sT), donde T es la constante de tiempo del sistema.
Usando el teorema del valor final,
Ganancia de estado estacionario = lim [1 / (1+sT)]
s→0 = 1 Usando el teorema del valor inicial, ganancia de estado transitorio = lim [1 / (1+sT)]
s→∞ = 0
Por lo tanto, la ganancia de estado estacionario de la función de escalón unitario es la unidad, mientras que su ganancia de estado transitorio es cero.
Publicaciones relacionadas:
Diferencia entre sistema de circuito abierto y circuito cerrado 
¿Propósito del radiador en el transformador? 
Transductor piezoeléctrico 
Explicación de la fuente de voltaje ideal y práctica 
Diodo de rueda libre o flyback: funcionamiento y propósito 
¿Qué es Cycloconverter?- Definición y Aplicaciones 
Motor CC sin escobillas (BLDC) 
j Operador y su significado 
Diferencia entre la eficiencia de rectificación y el factor de utilización del transformador 
Sistemas de accionamiento eléctrico 
Ventajas y desventajas del devanado de paso corto 
Motor sincrónico
