Parámetro Y de la red de dos puertos

El parámetro Y de la red de dos puertos es una matriz de admitancia de 2×2. Dado que la admitancia es la relación entre la corriente y el voltaje del circuito, esta matriz de admitancia proporciona la relación entre la corriente de entrada y salida y el voltaje de la red. También se conoce como parámetro de admitancia de cortocircuito.

El parámetro Y para una red de dos puertos se define como

[ I ] = [ Y ] [ V ]

donde [ Y ] es la matriz de admitancia, [ I ] y [ V ] son la matriz de corriente y tensión.

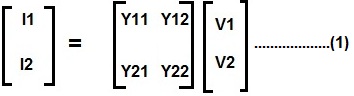
De la representación en forma de matriz anterior de la red de dos puertos, está claro que hay cuatro parámetros de admitancia, es decir, Y11, Y12, Y21 e Y22. Cada uno de ellos tiene un significado y significado especial que se discutirá más adelante en esta publicación.

Cálculo del parámetro Y:

Consideremos una red de dos puertos. Sean V1, I1, V2 e I2 el voltaje de entrada, la corriente de entrada, el voltaje de salida y la corriente de salida respectivamente.

La relación entre las cantidades de entrada y salida para la red anterior se obtiene usando (1) como se muestra a continuación.

I1 = Y11V1 + Y12V2 ……(2)

I2 = Y21V1 + Y22V2 …….(3)

Suponiendo que la salida de la red de dos puertos esté en cortocircuito, por lo tanto

V2 = 0

Ahora poniendo V2 = 0 en (2), obtenemos

I1 = Y11V1

Y11 = (I1 / V1)

De manera similar, poniendo V2 = 0 en (3), obtenemos

I2 = Y21V1

Y21 = (I2 / V1)

Nuevamente, suponiendo que el puerto de entrada de la red de dos puertos esté cortocircuitado, el voltaje de entrada será cero.

V1 = 0

Ahora poniendo V1 = 0 en (2), obtenemos

I1 = Y12V2

Y12 = (I1 / V2)

De manera similar, poniendo V1 = 0 en (3), obtenemos

I2 = Y22V2

Y22 = (I2 / V2)

Por lo tanto, hay cuatro parámetros Y para una red de dos puertos o cuatro terminales. Sus valores se tabulan a continuación.

Significado de diferente parámetro Y:

• Dado que Y11 es la relación entre la corriente y el voltaje de entrada cuando el puerto de salida está en cortocircuito, se conoce como admitancia del punto de activación de entrada.
• Y22 es la relación entre la corriente y el voltaje de salida cuando el puerto de entrada está en cortocircuito, por lo que se denomina admitancia del punto de conducción de salida de la red.
• Y12 es la relación entre la corriente de entrada y el voltaje de salida cuando el puerto de entrada está en cortocircuito, por lo que se denomina admitancia de transferencia inversa.
• Y21 es la relación entre la corriente de salida y el voltaje de entrada cuando el puerto de salida está cortocircuitado, por lo que se denomina admitancia de transferencia directa.

Representación de circuito equivalente del parámetro Y:

El circuito equivalente del parámetro Y para una red de dos puertos se puede representar usando (2) y (3) como se muestra a continuación.

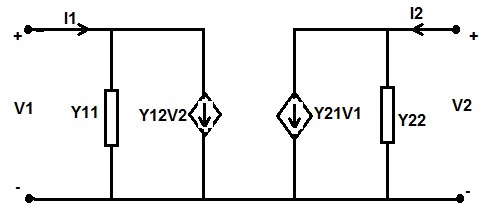
En el circuito anterior, las fuentes de corriente Y12V2 y Y21V1 se denominan fuente de corriente controlada por voltaje.

Problemas resueltos del parámetro Y:

Para comprender mejor el concepto discutido de parámetro Y, consideraremos un ejemplo.

Ejemplo:

Encuentre el parámetro Y para el circuito π que se muestra a continuación.

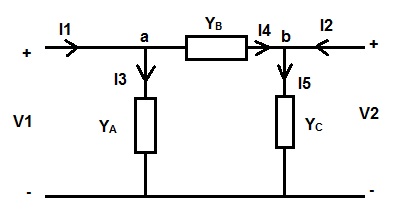
Solución:

Aplicar Ley de corriente de Kirchoff en el nodo ‘a’,

I1 = I3 + I4

= V1YA + (V1 – V2)YB

= (YA + YB)V1 + (-YB)V2

Así, I1 = (YA + YB)V1 + (-YB)V2

Pero de (2),

I1 = Y11V1 + Y12V2

Comparando las dos expresiones anteriores, obtenemos

Y11 = (YA + YB)

Y12 = -YB

Nuevamente, aplicando la Ley de Corriente de Kirchoff en el nodo ‘b’

I2 = I5 – I4

= YCV2 – (V1 – V2)YB

= (-YB)V1 + (YB + YC)V2

Por lo tanto,

I2 = (-YB)V1 + (YB + YC)V2

Pero de (3),

I2 = Y21V1 + Y22V2

Comparando las dos expresiones anteriores, obtenemos

Y22 = (YA + YB)

Y21 = -YB

Por lo tanto, los cuatro parámetros Y son

Y11 = (YA + YB), Y12 = -YB, Y22 = (YA + YB), Y21 = -YB (Responder)

Publicaciones relacionadas:

Ley de Gauss y su aplicación Diferencia entre aislador y disyuntor Efecto en la piel Régimen de Protección Unitario y No Unitario varistor ¿Cómo se eliminan los armónicos del voltaje generado por el alternador? Esfuerzo de tracción Teoría del sistema de arcos tierra-sin tierra Medida de Potencia Trifásica: Método de los Tres Vatímetros Activación por flanco y activación por nivel Error compuesto de CT: definición, cálculo y fórmula Devanado de armadura