Explicación del teorema de superposición

El teorema de superposición establece que la corriente resultante en cualquier rama de un red de revestimiento teniendo un número de fuentes, es la suma algebraica de la corriente que se produciría en él, cuando cada fuente actúa sola reemplazando a todas las demás fuentes independientes por su resistencia interna. Este teorema es muy útil para resolver una red que tiene dos o más fuentes que no están conectadas en serie ni en paralelo. Por lo tanto, una comprensión profunda del teorema de superposición es muy importante para lidiar con la teoría de circuitos. En este artículo, discutiremos el teorema de superposición, la aplicación, la fórmula y los pasos para resolver el problema.

El enunciado del teorema de superposición puede interpretarse como, si hay varias fuentes, ya sea una fuente de corriente o de voltaje en un circuito lineal, la corriente en cualquier rama del circuito se puede calcular asumiendo una fuente a la vez y reemplazando todas las demás fuentes por su resistencia interna. Básicamente, esto significa que una fuente de voltaje ideal debe cortocircuitarse, mientras que una fuente de corriente debe mantenerse en circuito abierto mientras se resuelve el problema relacionado con el teorema de superposición. Al calcular la corriente a través de cualquier rama en particular, se debe tener cuidado con la dirección de la corriente debido a la fuente individual para obtener la corriente total o resultante.

Índice de contenidos

Explicación del teorema de superposición:
Pasos para resolver la red usando el teorema de superposición:

Explicación del teorema de superposición:

Para comprender mejor el teorema de superposición, consideremos el circuito que se muestra a continuación.

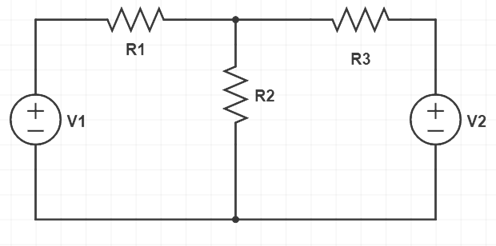
En este circuito hay dos fuentes V1 y V2. Ambas fuentes no están conectadas en paralelo ni en serie. Supongamos que queremos encontrar la corriente a través de la resistencia R2 usando el teorema de superposición.

Para aplicar el teorema, en primer lugar, reemplazamos cualquier fuente por su resistencia interna. Reemplacemos V2 primero. Dado que V2 es una fuente ideal, será reemplazada por un corto entre su terminal. Esto se muestra en la figura a continuación.

Se supone que la corriente a través de la resistencia R2 es I2 y puede calcularse como se muestra a continuación.

Como siguiente paso, desactivaremos la fuente V1 y la sustituiremos por un corto. Luego calcularemos nuevamente la corriente a través de la resistencia R2. La siguiente figura muestra este paso.

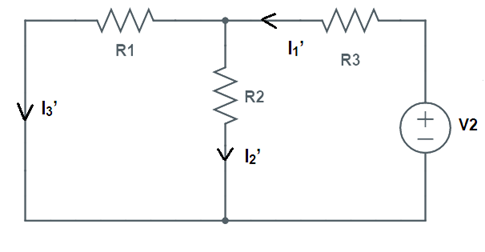
Busquemos ahora la corriente a través de la resistencia R2 debida únicamente a la fuente V2. Esta corriente se puede calcular de manera similar a como se calculó anteriormente.

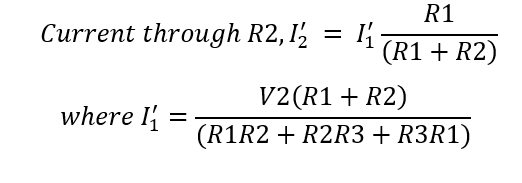
Por tanto, hemos calculado la corriente a través de la resistencia R2 debida a ambas fuentes cuando actúan solas. Ahora, según el teorema de superposición, la corriente resultante a través de R2 será la suma de I2 e I2′. Esto se debe a que la dirección de la corriente para ambas fuentes es la misma y, por lo tanto, se suman para obtener la corriente total. Si las corrientes hubieran sido en dirección opuesta, entonces deben haberse restado para obtener la corriente total.

Corriente resultante a través de R2

= I2 + I2′

Pasos para resolver la red usando el teorema de superposición:

Los pasos para resolver el circuito usando el teorema de superposición son bastante fáciles. Son los siguientes:

Paso 1: Tome solo una fuente independiente de voltaje/corriente y desactive todas las demás fuentes independientes. Para la fuente de voltaje, retire la fuente y cortocircuite las terminales del circuito respectivo y para las fuentes de corriente, simplemente elimine la fuente mientras mantiene sus terminales abiertas.

Calcule la corriente en la rama requerida del circuito cuando solo hay una fuente presente.

Paso 2: Repita el paso anterior para cada una de las fuentes independientes.

Paso 3: Para determinar la corriente de rama neta, sume las corrientes obtenidas en los dos pasos anteriores. Si la corriente obtenida en el Paso 1 y el Paso 2 están en la misma dirección, simplemente súmelas. Si las respectivas corrientes se dirigen de manera opuesta, entonces se deben restar las corrientes.