Impedancia característica de la línea de transmisión

La impedancia característica de una línea de transmisión se define como la raíz cuadrada de la relación entre la impedancia en serie por unidad de longitud por fase y la admitancia en derivación por unidad de longitud por fase. Si z e y son la impedancia en serie y la admitancia en derivación de la línea, la impedancia característica Zc se da como

Zc = √(z/y)

Donde z = R + jωL = impedancia en serie por unidad de longitud por fase

y = G + jωC = admitancia en derivación por unidad de longitud por fase

Tengamos una discusión detallada sobre la impedancia característica y algunos de los parámetros importantes asociados con la línea de transmisión. Para fines de análisis, consideramos una línea de transmisión larga. Sabemos que una línea de transmisión larga tiene Resistencia (R) e Inductancia (L) distribuidas en serie y Conductancia (G) y Capacitancia en derivación.

Conductancia en derivación (G) de línea básicamente representa la pérdida que ocurre debido a la corriente de fuga a lo largo de la cadena del aislador y la corona. En la línea eléctrica, este efecto suele ser muy pequeño y puede despreciarse.

Por lo tanto, para modelar una línea de transmisión larga, los parámetros asociados deben distribuirse en toda la longitud, como se muestra en la figura a continuación. Deje que la longitud de la línea sea ‘l’. Consideremos una pequeña sección de línea dx a una distancia x del extremo receptor.

Impedancia en serie de la sección dx = (impedancia en serie por unidad de longitud) dx

= zdx

Por lo tanto,

Caída de tensión en la sección dx = dv = (zdx)I

dV/dx = zI ……………………………..(1)

Ahora,

La corriente diferencial dI que fluye en la admitancia de derivación se puede encontrar multiplicando la admitancia de derivación y el voltaje V en la admitancia de derivación. Por eso,

dI = (ydx)V

dI/dx = yV ………………………….(2)

Diferenciando la ecuación (1) y (2) con x obtenemos,

d2V/dx2 = z(dI/dx) =yzV …….[ from equation (2)]

y d2I/dx2 = y(dV/dx)

= yzI ………[from equation (1)]

Para obtener el perfil de voltaje y corriente a lo largo de la línea, necesitamos resolver las dos ecuaciones diferenciales anteriores de segundo orden, suponiendo que se conocen el voltaje final de recepción Vr y la corriente Ir. También en el extremo receptor x = 0 ya que la sección diferencial dx se considera a una distancia x del extremo receptor. La solución general de la ecuación diferencial se da a continuación.

V = [(Vr +ZcIr)/2]eµx + [(Vr-ZcIr)/2]e-µx

yo = [(Vr/Zc) + Ir]eµx + [(Vr /Zc) + Ir]e-µx

Donde Zc = √(z/y) y µ = √yz

La constante Zc se denomina impedancia característica y µ se denomina constante de propagación. Características La impedancia y la constante de propagación son números complejos.

Índice de contenidos

Voltaje incidente y voltaje reflejado
Línea de transmisión plana o infinita

Voltaje incidente y voltaje reflejado

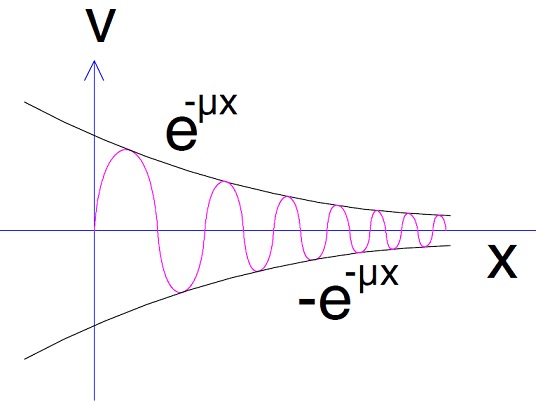
Observe cuidadosamente el perfil de tensión obtenido a lo largo de la línea de transmisión. Se compone de dos partes, [(Vr+ZcIr)/2]eµx y [(Vr-ZcIr)/2]e-µx. Dibujemos una gráfica de los dos componentes como se muestra en la figura a continuación.

Por encima de la parcela de [(Vr+ZcIr)/2]eµx muestra claramente que la magnitud del voltaje aumenta con el aumento de x. Esto significa que el voltaje desde el extremo receptor hasta el extremo emisor está aumentando. Esta parte del voltaje se conoce como voltaje incidente.

Por encima de la parcela de [(Vr-ZcIr)/2]e-µx revela que la magnitud del voltaje se reduce continuamente con el aumento de x. Esta parte del voltaje se conoce como voltaje reflejado.

Voltaje en cualquier punto = Voltaje incidente + Voltaje reflejado

Así podemos decir que, en una línea de transmisión el voltaje en cualquier punto es la suma del voltaje incidente y reflejado. El mismo proceso de pensamiento se aplica a la corriente y asumo que puedes hacerte una idea de la corriente por ti mismo.

Línea de transmisión plana o infinita

Una línea de transmisión plana se define como una línea terminada con una impedancia característica. Tal línea también se llama Línea de Transmisión Infinita. Dado que la línea termina con una impedancia característica, por lo tanto, Vr = ZcIr

Por lo tanto, el voltaje incidente en cualquier punto x en la línea = [(ZcIr +ZcIr)/2]eµx

= ZcIreµx

Sea µ = yz = a+jb donde a y b son constantes.

Por lo tanto, Voltaje incidente en cualquier punto x en la línea = ZcIre(a+jb)x

= ZcIreaxejbx

Magnitud del voltaje incidente = ZcIreax ya que la magnitud de ejbx es 1.

Voltaje reflejado en cualquier punto de la línea = [(Vr-ZcIr)/2]e-µx

= [(ZcIr – ZcIr)/2]e-µx

= 0

Así un piso o infinito la línea no tiene voltaje reflejado sino solo voltaje incidente. Esto también puede ser aunque de otra manera ridícula. Si la línea tiene una longitud infinita, ¿cómo puede tener un voltaje reflejado? ¿De dónde se reflejará? Entonces no hay voltaje reflejado en línea infinita o plana.