Triángulo de impedancia

Definición:

El Triángulo de Impedancia es un triángulo rectángulo cuya base, perpendicular e hipotenusa representan la Resistencia, la Reactancia y la Impedancia respectivamente. Es básicamente una representación geométrica de la impedancia del circuito.

Explicación del Triángulo de Impedancia:

La impedancia consta de dos componentes a saber. resistencia y reactancia. Por lo tanto, se puede expresar en estos dos componentes. Deje que la impedancia de un circuito de corriente alterna sea Z = R+jX donde R y X representan la resistencia y la reactancia. Está claro de la expresión de Z es que, es un Número complejo y por lo tanto puede representarse geométricamente de la misma manera que un número complejo. La representación geométrica se muestra a continuación.

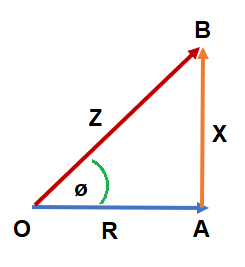
El triángulo anterior OAB así formado se llama Triángulo de impedancia. A partir de este triángulo, la magnitud de la impedancia Z se puede encontrar fácilmente usando el Teorema de Pitágoras. La magnitud de la impedancia Z es igual a OB y ​​se puede encontrar a continuación.

OB2 = OA2+AB2

Z2 = R2+X2

Por lo tanto, podemos decir que el cuadrado de la impedancia es igual a la suma del cuadrado de la resistencia y la reactancia.

Z = √(R2+X2)

El ángulo que forma Z con R, es decir, el ángulo entre OA y OB se puede encontrar como

tanƟ = (X/R)

Por lo tanto, el Triángulo de impedancia nos ayuda a encontrar la magnitud y el ángulo de impedancia de un circuito.

Significado:

El Triángulo de impedancia es muy útil si desea encontrar el valor de la impedancia. Este triángulo también se puede utilizar para encontrar el valor del factor de potencia. Estos valores se pueden averiguar si se conoce la impedancia en forma compleja. Entenderemos esto con un ejemplo.

Deje que la impedancia de un circuito particular se dé como Z = 8+j6. Queremos saber la magnitud de la impedancia y el factor de potencia. Estos valores pueden calcularse como sigue.

Z = √(82+62)

= 10 Ω

Para calcular el factor de potencia, dibujaremos un triángulo de impedancia (consulte el triángulo que se muestra anteriormente en el artículo. Asigne OA = 8 Ω y AB = 6 Ω) y luego encontraremos el cosø. Dado que el factor de potencia es igual al coseno del ángulo entre Z y R, este valor de cosø es igual al factor de potencia.

cosø = (R/Z)

=(8/10)

= 0,8

Publicaciones relacionadas:

Motor de inducción de arranque por condensador ¿Qué es la magnetorresistividad y los magnetorresistores? Cable a tierra / Cable Sky / Cable blindado en la línea de transmisión Diferencia entre motor y generador Resta en complemento a 2 de números binarios Operación en paralelo de un transformador Motor de condensador dividido permanente (PSC) Factor de capacitancia y disipación Diferencia entre la banda de valencia y la banda de conducción Teorema del valor inicial Diferencia entre armónicos y subarmónicos Relé electromagnético