Fórmula y derivación de la frecuencia resonante

La fórmula de frecuencia de resonancia para el circuito de resonancia en serie y en paralelo que consta de resistencia, inductor y condensador es diferente. En este artículo, repasaremos la resonancia. frecuencia fórmula para el circuito de resonancia en serie y en paralelo y su derivación. También discutiremos el método para encontrar la frecuencia resonante para cualquier circuito dado con la ayuda de algunos ejemplos.

Fórmula de frecuencia resonante: circuito de resonancia en serie

La fórmula para la frecuencia de resonancia para un circuito de resonancia en serie se da como

f = 1/2π√(LC)

Derivación:

Consideremos una conexión en serie de R, L y C. Esta conexión en serie está excitada por una fuente de CA.

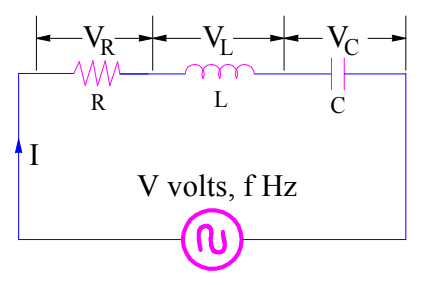
Primero calculemos la impedancia Z del circuito.

Z = R + jωL – j/ωC

= R + j(ωL – 1/ ωC)

Bajo la condición de resonancia, el circuito es puramente resistivo. Esto significa que la parte imaginaria de la impedancia Z será cero durante la condición de resonancia oa la frecuencia resonante. Siempre debe tener esto en cuenta al calcular la frecuencia de resonancia para un circuito dado.

Esto significa,

(ωL – 1/ ωC) = 0

ωL = 1/ωC

ω2 = 1/(LC)

ω = 1/(LC)

Como sabemos que

ω = 1/2πf

Por lo tanto, f = 1/2πω

Frecuencia de resonancia (f0) para circuito de resonancia en serie,

Tenga en cuenta que no es necesario dibujar un diagrama fasorial. Solo necesita encontrar la impedancia y hacer parte imaginaria de impedancia cero para encontrar la frecuencia resonante del circuito dado. También aplicaremos la misma técnica para el circuito de resonancia en paralelo.

Fórmula de frecuencia resonante: circuito de resonancia paralelo

La fórmula para la frecuencia de resonancia para un circuito de resonancia paralelo se da como,

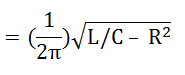
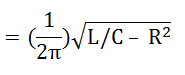
Derivación:

Consideremos un circuito de resonancia paralelo como se muestra a continuación. Nuestro objetivo es encontrar la fórmula de frecuencia resonante para este circuito.

Nuevamente, primero que nada, encontraremos la impedancia Z del circuito.

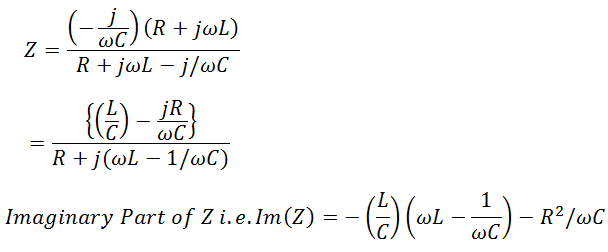
Igualando la parte imaginaria a cero, obtenemos

⇒ -(ωL2)/C + L/(ωC2) – R2/(ωC) = 0

⇒ -ω2L2C + L – R2C = 0

⇒ ω2L2C = L – R2C

⇒ ω2 = 1/(LC) – R2/L2

Ya que, ω = 1/2πf

Frecuencia de resonancia f0

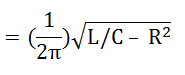
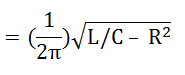
Entonces, ¿qué tan simple es encontrar el valor de la frecuencia de resonancia? ¿no es así? Resolvamos algún ejemplo para tener una mejor comprensión.

Ejemplo:

Encuentre la frecuencia de resonancia para el circuito que se muestra en la siguiente figura.

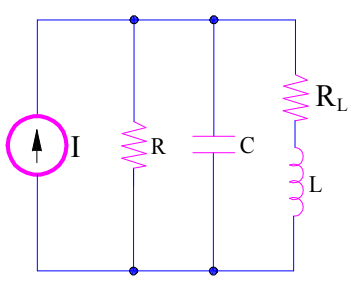
Los valores RL, L, R y C son 1 Ohm, 1 Henry, 0.5 Farad y 1 Ohm respectivamente.

Solución:

Como se discutió, en primer lugar, encontraremos la impedancia y luego igualaremos la parte imaginaria de Z a cero para obtener el valor de la frecuencia resonante. Pero, seamos un poco más inteligentes. Como el circuito es una conexión de elementos en paralelo, es mejor encontrar la Admitancia Y en lugar de la impedancia para facilitar el cálculo.

Y = 1/R + jωC + 1/(RL+jωL)

= 1/R + jωC + (RL – jωL)/(RL2+ω2L2)

Parte imaginaria de Y

= ωC – ωL/(RL2+ω2L2)

Para obtener la frecuencia de resonancia, haga que la parte imaginaria de la admitancia sea cero.

ωC – ωL/(RL2+ω2L2) = 0

(RL2+ω2L2) = L/C

ω2 = (1/LC) – (RL2 / L2)

Ahora, pon el valor de C, L y RL

ω2 = 1

ω = 1 rad/seg. (Respuesta)

Publicaciones relacionadas:

Diferencia entre período y frecuencia Sag en línea aérea de transmisión y su cálculo Transformadores elevadores y reductores Relación de cortocircuito: definición, cálculo y significado Transistor NPN Amperímetro Shunt – Construcción y Cálculo Potencia Activa, Reactiva y Aparente Diferencia entre el tipo de núcleo y el transformador tipo carcasa Motores de fase dividida con condensador o arranque de motor de inducción monofásico por condensador Diferencia entre retroalimentación positiva y negativa Principio básico del transformador automático Tipos de fusibles