¿Qué es el teorema de reciprocidad?

El teorema de reciprocidad establece que el valor de la corriente debido a una sola fuente en cualquier rama particular del circuito es igual al valor de la corriente en la rama original donde se colocó la fuente cuando la fuente se cambia a esa rama particular del circuito. Este teorema solo es aplicable para una red recíproca, es decir lineal y circuito bilateral que tiene una sola fuente independiente. Sin embargo, este teorema se puede usar tanto para circuitos de CA como de CC.

Índice de contenidos

Explicación del teorema de reciprocidad:
Pasos para usar el Teorema de Reciprocidad:

Explicación del teorema de reciprocidad:

El enunciado del teorema de la reciprocidad parece un poco confuso, pero espera, explicaré este teorema aquí en detalle para que te quede muy claro. Consideremos el siguiente circuito.

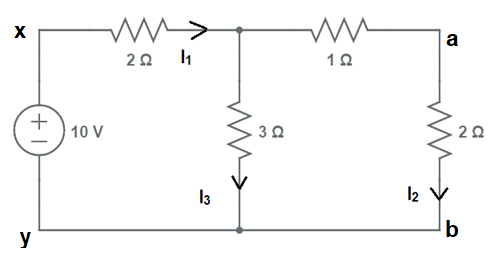
Comprobemos primero si podemos aplicar el teorema de no. Dado que el circuito es una red bilateral lineal y, por lo tanto, recíproca. Por lo tanto, podemos aplicar el teorema de reciprocidad en este circuito.

Supongamos que queremos comprobar la validez del teorema de reciprocidad en la rama xy y ab. Para esto, primero encontramos la corriente a través de la rama ab como se muestra a continuación.

Resistencia equivalente entre xy

= (3×3)/6 + 2

= 3,5 Ω

Por lo tanto, la corriente I1

= 10/3,5A

= 2,86 A

Ahora, la corriente a través de la rama ab se puede calcular usando la regla de división actual como se muestra a continuación.

I2 = (3x I1)/(3+3)

= 2,86/2

=1,43 A

Ahora cambiemos la posición de la fuente de voltaje y colóquela en la rama ab. Esto se muestra en la figura a continuación.

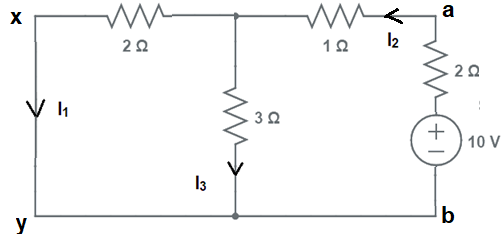
Nuestro objetivo es encontrar el valor de la corriente en la rama xy, es decir, la rama donde se colocó originalmente la fuente cuando se cambia a la rama particular ab donde calculamos la corriente.

Primero encontremos la resistencia equivalente entre los terminales ab primero. Esta resistencia se calcula de la siguiente manera.

Resistencia equivalente entre terminales xy

= 2+1+6/5

= 4,2 Ω

Corriente I2 = 10/4.2

= 2,38 A

Usando la regla de división actual, la corriente en la rama xy se puede encontrar como se muestra a continuación.

I1 = (2,38×3)/5

= 1,43 A

Observe cuidadosamente el valor de las corrientes I1 e I2. ¿No son iguales? Son lo mismo.

Así, el Teorema de la Reciprocidad se puede entender de otra manera. En electricidad, la causa es voltaje y el efecto es corriente. Esto simplemente significa que el voltaje hace que la corriente fluya. Llamemos tensión a la excitación y corriente a la respuesta. Está claro del ejercicio anterior que, intercambiar la posición de excitación y respuesta no altera el valor de la respuesta.

El teorema de reciprocidad se puede establecer como: la relación de excitación y respuesta permanece constante incluso si intercambiamos la posición de excitación y respuesta en una red recíproca. Esta definición coincide con la significado literal de la palabra “reciprocidad”.

Pasos para usar el Teorema de Reciprocidad:

Paso 1: como primer paso, verifique si el circuito dado es una red bilateral lineal (circuito recíproco) que tiene una sola fuente o no. Si el circuito tiene más de una fuente, este teorema no se puede aplicar. Por lo tanto, ya ha terminado con su trabajo. Si el circuito es recíproco, siga los siguientes pasos.

Paso 2: seleccione la rama entre la que se comprobará la reciprocidad.

Paso 3: Encuentre el valor de la corriente en la rama utilizando el análisis de red convencional.

Paso 4: La fuente de voltaje se intercambia entre las ramas en cuestión.

Paso 5: Calcule la corriente en la rama donde existía anteriormente la fuente de voltaje.

Paso 6: Verifique que la corriente calculada en el paso 3 y el paso 5 sea la misma. Si son iguales, significa que se valida la reciprocidad entre las ramas involucradas.

Espero que hayas entendido el concepto. En caso de duda, escriba amablemente en la caja de comentarios. Tu voz será escuchada y respondida.