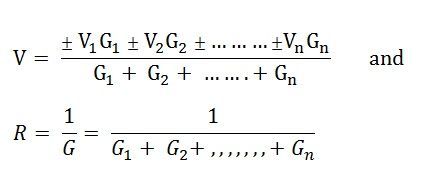los Teorema de Millman establece que – cuando varias fuentes de voltaje (V1, V2, V3……… Vn) están en paralelo con resistencia interna (R1, R2, R3………….Rn) respectivamente, el arreglo puede reemplazarse por un solo voltaje equivalente fuente V en serie con una resistencia en serie equivalente R. En otras palabras; determina el voltaje a través de las ramas paralelas del circuito, que tienen más de una fuente de voltaje, es decir, reduce la complejidad del circuito eléctrico.
Este teorema es dado por Jacob Millman. La utilidad de Teorema de Millman es que el número de fuentes de voltaje en paralelo se puede reducir a una fuente equivalente. Es aplicable solo para resolver la rama paralela con una resistencia conectada a una fuente de voltaje o fuente de corriente. También se utiliza para resolver redes que tienen un circuito de puente desequilibrado.
Índice de contenidos
Explicación del teorema de Millman
Suponiendo una red de CC de numerosas fuentes de voltaje paralelas con resistencias internas que suministran energía a una resistencia de carga RL como se muestra en la figura a continuación
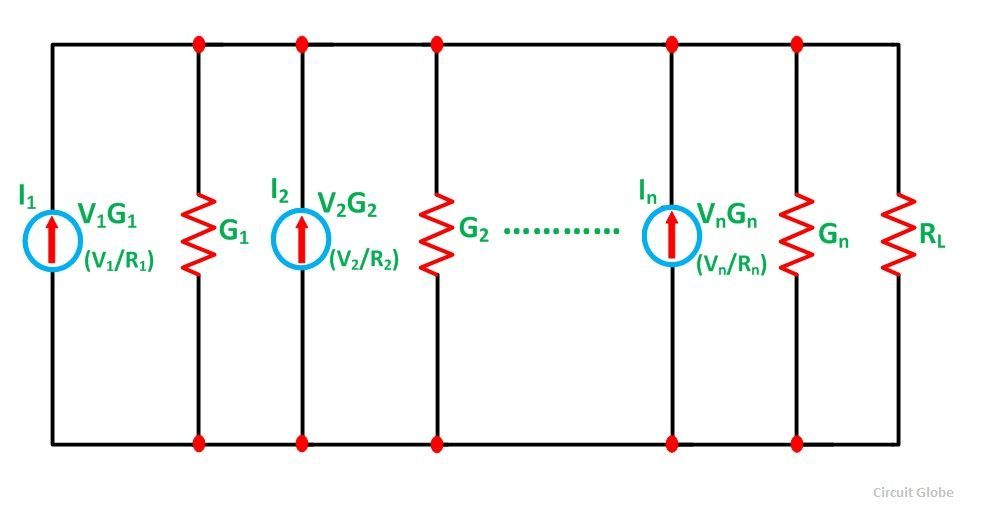 Deje que I represente la corriente resultante de las fuentes de corriente paralelas mientras que G la conductancia equivalente como se muestra en la figura a continuación
Deje que I represente la corriente resultante de las fuentes de corriente paralelas mientras que G la conductancia equivalente como se muestra en la figura a continuación
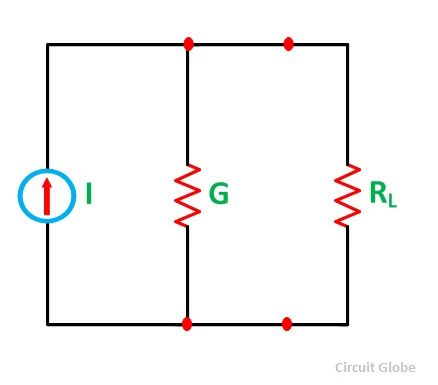
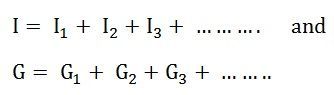
A continuación, la fuente de corriente resultante se convierte en una fuente de voltaje equivalente, como se muestra en la siguiente figura.
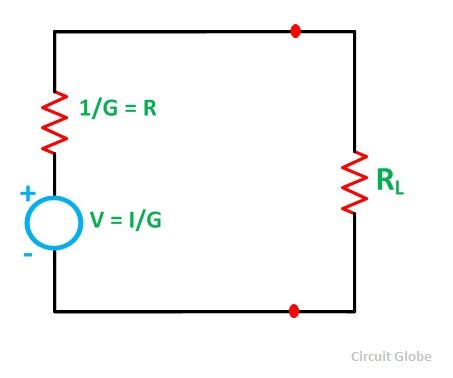 Por lo tanto,
Por lo tanto,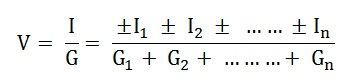
Los signos positivo (+) y negativo (-) parecían incluir los casos en los que las fuentes pueden no estar suministrando corriente en la misma dirección.
También,
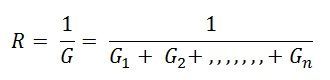
Y como sabemos,
I = V/R, y también podemos escribir R = I/G como G = I/R
Entonces la ecuación se puede escribir como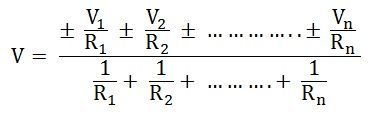
Donde R es la resistencia equivalente conectada a la fuente de voltaje equivalente en serie.
Por lo tanto, la ecuación final se convierte en
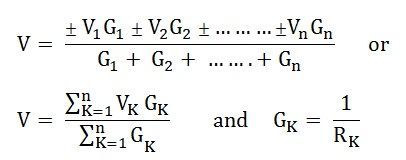
Pasos para resolver el teorema de Millman
Los siguientes pasos se utilizan para resolver la red por el teorema de Millman
Paso 1 – Obtenga la conductancia (G1, G2,….) de cada fuente de tensión (V1, V2,….).
Paso 2 – Encuentre el valor de la conductancia equivalente G eliminando la carga de la red.
Paso 3 – Ahora, aplique el teorema de Millman para encontrar la fuente de voltaje equivalente V mediante la ecuación que se muestra a continuación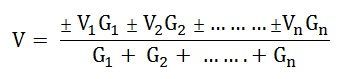
Etapa 4 – Determine la resistencia en serie equivalente (R) con las fuentes de tensión equivalentes (V) mediante la ecuación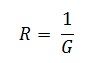
Paso 5 – Encuentre la corriente IL que fluye en el circuito a través de la resistencia de carga RL mediante la ecuación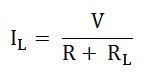

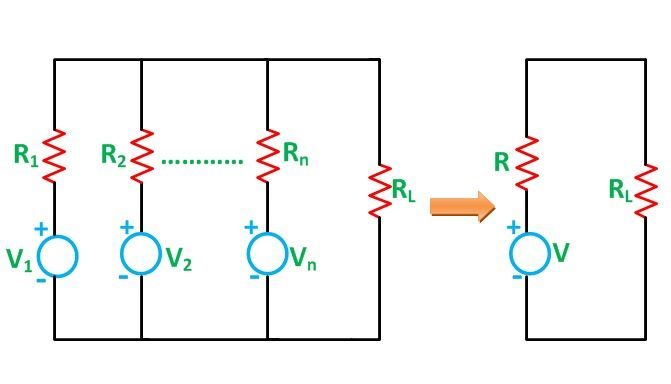 Según el teorema de Millman
Según el teorema de Millman