Error límite y error límite relativo

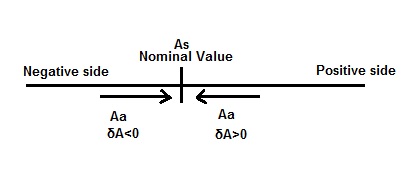
<p style=”text-align: justify;”>El error límite se define como la desviación máxima, ya sea en el lado positivo o en el lado negativo, en la medición por un instrumento del valor nominal o el valor real. Supongamos que el valor verdadero o valor nominal de una cantidad es As y el valor medido por el instrumento es Aa, entonces

Error límite δA = (Aa – As).

El valor medido puede ser mayor que el valor real As o menor que As. Por lo tanto, δA será positivo o negativo. Esta es la razón por la que el error límite se especifica como ± δA. Este error también se conoce como error de garantía, ya que se garantiza que el error en la medición se encuentra dentro de los límites especificados.

Por ejemplo, el valor nominal de una resistencia es de 100 Ω con un error límite de ±10 Ω. La magnitud de la medida estará entre los límites, (100±10) Ω, es decir, 90 y 110 Ω. Por lo tanto, se garantiza que la medición de la resistencia por parte del instrumento estará entre 90 y 110 Ω.

Importancia del error límite:

La precisión de un instrumento depende de varios factores como el material, el diseño y la mano de obra. Diferentes instrumentos tienen diferente precisión y, por lo tanto, limitan el error. Cuanto mayor sea la precisión, menor será el error límite. Pero no es aconsejable usar materiales y diseños delicados para cada instrumento. En realidad, la selección del instrumento depende de la aplicación. Por ejemplo, si queremos medir el peso de frutas, no necesitaremos tener una báscula para pesar oro. Esto significa que la selección de un instrumento depende del grado de precisión requerido. Por lo tanto, al elegir un instrumento, se debe hacer un compromiso entre el error límite y el grado de precisión requerido. El fabricante generalmente especifica el error límite en términos de porcentaje del valor nominal de la cantidad o desviación de escala completa.

Error límite relativo o error límite fraccional:

El error límite relativo o fraccional es la relación entre el error y la magnitud del valor nominal de la cantidad. Por lo tanto,

Error límite relativo εr = δA / As ….(1)

El error límite relativo se expresa en porcentaje y, por lo tanto,

% error límite relativo = (δA / As)x100

Ahora de (1),

δA = εrAs ………(2)

Pero el valor real o valor límite de medición,

Aa = As± δA

Por eso,

Aa = As± εrAs [from (2)]

= (1+εr)Como

Consideremos ahora algunos ejemplos para comprender mejor el error límite relativo.

Ejemplo 1:

Un voltímetro de 0-150 V tiene un error límite del 1% de la lectura de escala completa. El voltaje medido por el instrumento es de 75 V. Calcular el error límite en porcentaje.

Solución:

El error límite del voltímetro es del 1 % para la lectura de escala completa. Esto significa que el error será (1/100) de 150 = 1,5 V cuando el voltímetro marque 150 V. Como el error límite de un instrumento es el mismo a menos que lo mencione el fabricante, esto significa que el error de medición será de 1,5 V para cada y cada medida.

Por lo tanto, cuando la lectura es de 75 V, el error seguirá siendo de 1,5 V. Por lo tanto, el % de error límite

= (1.5/75)x100 = 2%

Tenga en cuenta que el error límite porcentual es el doble del valor mencionado en la lectura de escala completa. El error límite aumenta a medida que disminuye la lectura del voltímetro. Si la lectura es de 37,5 V, el porcentaje de error será del 4 %. Este aumento del error se debe al hecho de que la magnitud del error es constante a 1,5 V independientemente de la lectura.

Por lo tanto, se debe elegir la precisión a escala completa si la lectura de cantidad requerida en una aplicación está cerca de la lectura de escala completa del instrumento.

Ejemplo-2:

A vatímetro teniendo un rango de 1000 W tiene un error del 1% del valor verdadero. Encuentre el error límite porcentual cuando la potencia real es de 100 W.

Solución:

Tenga en cuenta aquí que el error se da en términos de porcentaje del valor real. Esto significa que el error no es un valor constante, sino que cambiará a medida que cambie la lectura del instrumento (la lectura cambia según la potencia real). Cuando la verdadera potencia es de 100 W, el error es 1% de 100 = 1 W. Así, el potencia medida será entre 99 y 101 W.

Por lo tanto, si la aplicación requiere medir un amplio rango, se considerará el error en términos de porcentaje del valor real.

Publicaciones relacionadas:

Diferencia entre período y frecuencia Sag en línea aérea de transmisión y su cálculo Transformadores elevadores y reductores Relación de cortocircuito: definición, cálculo y significado Clases de enfriamiento de transformadores Diferencia entre electricidad estática y actual Diferencia entre voltaje de arco, voltaje de reencendido y voltaje de recuperación Transformación de fuente Sistema Trifásico Factor Q / Factor de calidad de una bobina Teorema de DeMorgan Control de velocidad VVVF del motor de inducción