Índice de contenidos
Inductancia mutua
La inductancia mutua se define como la inductancia de un circuito causada por el acoplamiento mutuo con otro circuito. El acoplamiento mutuo de dos bobinas significa que el campo magnético producido por una bobina está uniendo/cruzando la otra bobina y viceversa. La inductancia mutua generalmente se denota con la letra M y su unidad SI es Henry.
Tomemos un ejemplo para una mejor comprensión de esta inductancia mutua. Supongamos que la corriente I fluye en una bobina 1 y otra bobina 2 se mantiene cerca de la bobina de modo que su centro esté en una línea.

Dado que la corriente en la bobina 1 fluye en sentido contrario a las agujas del reloj cuando se ve desde el lado del interruptor (S). Por lo tanto, según la ley de tornillo, el campo magnético producido por la bobina será perpendicular a la bobina 1 y hacia el espectador. Este campo magnético producido por la bobina 1 obviamente enlazará o pasará a través de otra bobina 2. Si este campo magnético cambia con el tiempo, entonces cambiará el flujo a través de la bobina 2. Por lo tanto, según la Ley de inducción electromagnética de Faraday, se inducirá una fem en la bobina 2. Esta fem se inducirá de tal manera que se oponga a la causa, es decir, el campo magnético cambiante según la Ley de Lenz.
Si el flujo magnético Ø se vincula con la bobina 2, la inductancia mutua de la bobina 2 se da como
M2 = Ø / I …………………(1)
Ahora suponga que la batería y el interruptor están conectados a la bobina 2 mientras se mantienen iguales todos los demás parámetros, como la geometría de la bobina, el espaciado, etc. En este caso, el flujo magnético debido a la bobina 2 también será Ø. Este flujo conectará la bobina 1 y, por lo tanto, se generará una fem en la bobina. De esta forma, la inductancia mutua de la bobina 1 estará dada por
M2 = Ø / I …………………..(2)
De las dos ecuaciones anteriores vemos que la inductancia mutua de ambas bobinas es la misma si se mantiene la geometría de las bobinas. Cabe señalar que la inductancia mutua solo depende de la geometría, como el radio de la bobina, el número de vueltas, el espacio entre las dos bobinas, etc., como la autoinducción.
Acoplamiento perfecto o acoplamiento 100% mutuo
Cuando todo el campo magnético producido por una bobina se une o se acopla con la otra bobina, se dice que el acoplamiento entre las bobinas es perfecto o 100 % de acoplamiento mutuo entre las bobinas. Pero en realidad siempre existe alguna fuga de flujo y, por lo tanto, el 100% o el acoplamiento mutuo perfecto es solo un concepto. Consideremos un circuito simple como se muestra en la figura a continuación.
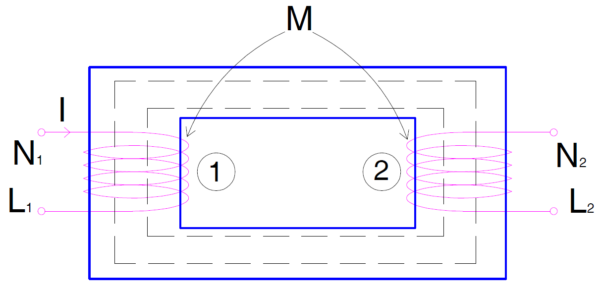
El flujo creado por la bobina 1 que tiene N1 número de vueltas es Ø. Si se supone que la fuga de flujo es cero, entonces todo el Ø del flujo se conectará con la bobina 2 que tiene N2 vueltas. Por lo tanto, la inductancia mutua M21 de la bobina 2 se da como
M21 = Inductancia Mutua de la Bobina 2 debido a la corriente en la Bobina 1
= Enlace de flujo total de la bobina 2 / Corriente en la bobina 1
= N2 Ø21 / I1
Pero Ø21 = BA
Ø21 = [(µ0µrN1I1/L) x A] / I1
= µ0µrN1A/L
Por lo tanto,
M21 = µ0µrN1N2A/L ………………….(3)
Ahora suponga que la misma corriente I2 fluye a través de la bobina 2 de manera que el flujo producido por la bobina 2 es Ø (suponiendo que el área de la sección transversal y la longitud de ambas bobinas son iguales). La inductancia mutua de la bobina 1 se da entonces como
M12 = Inductancia Mutua de la Bobina 1 debido a la corriente en la Bobina 2
= Enlace de flujo total de la bobina 1 / Corriente en la bobina 2
= N1 Ø12 / I2
Pero Ø12 = bobina de enlace de flujo 1 debido al campo magnético creado por la bobina 2
= BA
⇒Ø12 = [(µ0µrN2I2/L) x A] / I2
= µ0µrN1N2A/L
Por lo tanto,
M12 = µ0µrN1N2A/L ………………….(4)
De la ecuación (3) y (4) observamos que, para un acoplamiento mutuo perfecto, la inductancia mutua de ambas bobinas es la misma.
M12 = M21 = M = µ0µrN1N2A/L
El concepto de acoplamiento mutuo se usa ampliamente en muchas máquinas eléctricas como transformadores, motores, generadores, etc.
Relación entre autoinducción e inductancia mutua
Deje que la autoinductancia de la bobina 1 sea L1 y la de la bobina 2 sea L2. Por lo tanto
L1 = µ0µrN12A/L
L2 = µ0µrN22A/L
Multiplicando lo anterior, obtenemos
L1L2 = (µ0µrN1N2A/L) x (µ0µrN1N2A/L)
= METRO x METRO
= M2
Así, para un acoplamiento mutuo del 100 %,
M2 = L1L2
Coeficiente de Acoplamiento o Factor de Acoplamiento
Como se discutió anteriormente en la publicación, el acoplamiento perfecto o el 100 % de acoplamiento mutuo es solo un concepto. Siempre hay alguna fuga de flujo magnético, aunque tratamos de tener la mínima fuga posible. Por lo tanto, una fracción del flujo magnético generado por una bobina solo se une con otra bobina. Por esta razón, el coeficiente de acoplamiento o factor de acoplamiento entró en escena.
Coeficiente de acoplamiento / Factor de acoplamiento denota la fracción de acoplamiento o la fracción de flujo que une la segunda bobina debido al flujo de corriente en una bobina. Por lo general, se denota con la letra k. El valor de k se da como
k = METRO / √(L1L2)
El valor de k varía de 0 a 1, es decir 0 ≤k≤1
- Si el valor de k es 1 entonces las dos bobinas están perfectamente acopladas o 100% acopladas entre ellas.
- Si k > 0,5, se dice que las dos bobinas están estrechamente acopladas.
- Si k <0,5, se dice que las dos bobinas o el circuito están débilmente acoplados.
| Tipo de acoplamiento | Valor del Coeficiente de Acoplamiento (k) |
| Acoplamiento perfecto | 1 |
| Circuito estrechamente acoplado | >0.5 |
| Circuito débilmente acoplado | <0.5 |