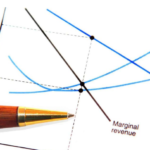
Alternar angulos interiores: Un ángulo se forma cuando dos rayos, una línea con un punto final, se encuentran en un punto llamado vértice. El ángulo está formado por la distancia entre los dos rayos. Los ángulos en geometría a menudo se denominan mediante el símbolo de ángulo, por lo que el ángulo A se escribiría como ángulo A.
A ángulo recto, también llamado ángulo plano, está formado por una línea recta. La medida de este ángulo es de 180 grados. Un ángulo recto también puede estar formado por dos o más ángulos que sumen 180 grados. Aquí, ángulo 1 + ángulo 2 = 180.A linea transversal es una línea que cruza o pasa por otras dos líneas. A veces, las otras dos líneas son paralelas y la transversal pasa por ambas líneas en el mismo ángulo. Las otras dos líneas no tienen que ser necesariamente paralelas para que una transversal las cruce.
 Definición de ángulos alternos interiores
Definición de ángulos alternos interiores
Alternar angulos interiores Ángulos interiores se forman cuando una transversal pasa a través de dos líneas. El ángulo que se forma en lados opuestos de la transversal y dentro de las dos líneas es ángulo interior alterno. Observe los pares de ángulos azul y rosa. Lineas paralelas son dos líneas en un plano bidimensional que nunca se encuentran ni se cruzan. Cuando una transversal pasa a través de líneas paralelas, existen propiedades especiales sobre los ángulos que se forman que no ocurren cuando las líneas no son paralelas. Observe las flechas en las líneas myn hacia la izquierda. Estas flechas indican que las líneas myn son paralelas.
Índice de contenidos
Definición de ángulos alternos interiores
Los ángulos que se forman dentro de las dos líneas paralelas, cuando se cortan por una transversal, son iguales a sus pares alternos.

En la figura anterior, puede ver, dos líneas paralelas están intersectadas por una transversal. Por lo tanto, los ángulos alternos dentro de las líneas paralelas serán iguales.
es decir. ∠A = ∠D y ∠B = ∠C
¿Qué son los ángulos alternos internos / Teorema inverso de los ángulos internos?
El teorema establece que “si una transversal cruza el conjunto de líneas paralelas, los ángulos alternos internos son congruentes”.
Dado: a // b
Probar: ∠4 = ∠5 y ∠3 = ∠6
Prueba: Suponga que ayb son dos rectas paralelas y que l es la transversal que interseca a y b en los puntos P y Q. Vea la figura.

A partir de las propiedades de la línea paralela, sabemos que si una transversal corta dos líneas paralelas cualesquiera, los ángulos correspondientes y los ángulos verticalmente opuestos son iguales entre sí. Por lo tanto,
∠2 = ∠5 ……… .. (i) [Corresponding angles]
∠2 = ∠4 ……… .. (ii) [Vertically opposite angles]
De la ecuación (i) y (ii), obtenemos;
∠4 = ∠5 [Alternate interior angles]
Similar,
∠3 = ∠6
Por lo tanto, está probado.
Antítesis del teorema
Si los ángulos interiores producidos por la línea transversal en dos coplanares son congruentes, entonces las dos líneas son paralelas entre sí.
Dado: ∠4 = ∠5 y ∠3 = ∠6
Para demostrar: a // b
Prueba: Dado que ∠2 = ∠4 [Vertically opposite angles]
Entonces, podemos escribir
∠2 = ∠5, que son ángulos correspondientes.
Por lo tanto, a es paralelo a b.
¿Qué es un ángulo interior alterno?
Alternar angulos interiores son congruentes. Formalmente, estas son dos Ángulos interiores que se encuentran en diferentes líneas paralelas y en lados opuestos de una
¿Cuál es el ángulo en los segmentos alternos? los segmento alternativo teorema (también conocido como el teorema de la cuerda tangente) establece que en cualquier círculo, el ángulo entre un acorde y una tangente a través de uno de los puntos finales del acorde es igual a la ángulo en el segmento alternativo. En el diagrama anterior, el anglos del mismo color son iguales entre sí.
. Corte de líneas paralelas. por una transversal.
¿Son iguales los ángulos alternos internos?
Alternar angulos interiores se forman cuando una transversal pasa a través de dos líneas. los anglos que se forman en lados opuestos de la transversal y dentro de las dos líneas son ángulos alternos internos. El teorema dice que cuando las rectas son paralelas, la Alternar angulos interiores son iguales.
Lea también: Resumen de Antigone
¿Cuál es el ángulo en el segmento alternativo?
los segmento alternativo teorema (también conocido como el teorema de la cuerda tangente) establece que en cualquier círculo, el ángulo entre un acorde y una tangente a través de uno de los puntos finales del acorde es igual a la ángulo en el segmento alternativo. En el diagrama anterior, el anglos del mismo color son iguales entre sí.
Ángulos interiores alternos congruentes
los Teorema de los ángulos interiores estados, si dos rectas paralelas son cortadas por un transversal, entonces los pares de ángulos alternos internos son congruentes.
A teorema es una afirmación probada o una idea aceptada que se ha demostrado que es cierta. los conversar de este teorema, que es básicamente el opuesto, también es un enunciado probado: si dos líneas están cortadas por una transversal y los ángulos alternos internos son congruentes, entonces las líneas son paralelas.
Estos teoremas se pueden usar para resolver problemas de geometría y encontrar información faltante. Este diagrama muestra qué pares son iguales y alternos en el interior. Observe que las líneas son paralelas.