La derivada de ln x – Parte del cálculo es memorizar las reglas derivadas básicas como la regla del producto, la regla de la potencia o la regla de la cadena. Una de las reglas que verá surgir a menudo es la regla para la derivada de ln x. En la siguiente lección, veremos algunos ejemplos de cómo aplicar esta regla para encontrar diferentes tipos de derivadas. También veremos cómo el uso de las leyes de los logaritmos puede facilitar aún más la obtención de este tipo de derivadas.
Veamos nuestro primer método, la regla de la cadena. ¿Cómo funciona la regla de la cadena? Bueno, en primer lugar, la regla de la cadena es una fórmula para calcular la composición de dos o más funciones. Digamos que tenemos una función con un argumento complicado, como sin x2. La función es seno y el argumento es x2. Si el argumento fuera simplemente x, diferenciaríamos sen x y obtendríamos cos x.
Índice de contenidos
Derivada de ln x
La derivada de ln (x) es una derivada bien conocida. Esta lección nos mostrará los pasos necesarios para encontrar esta derivada y repasará una aplicación del mundo real que involucra la derivada de ln (x).
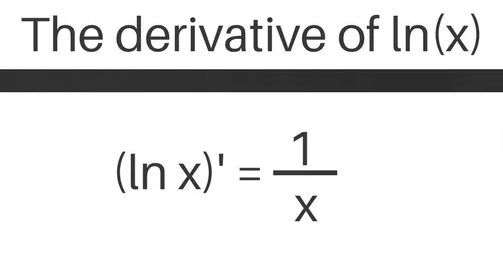Derivada ln x
Derivada de Ln (x) Pasos para resolver
Queremos encontrar la derivada de ln (x). La derivada de ln (x) es 1 / x y en realidad es una derivada bien conocida que la mayoría recuerda. Sin embargo, siempre es útil saber de dónde proviene esta fórmula, así que echemos un vistazo a los pasos para encontrar esta derivada.
Para encontrar la derivada de ln (x), lo primero que hacemos es dejar y = ln (x). A continuación, usamos la definición de un logaritmo para escribir y = ln (x) en forma logarítmica. La definición de logaritmos establece que y = log b (x) es equivalente a b y = x. Por lo tanto, por la definición de logaritmos y el hecho de que ln (x) es un logaritmo con base e, tenemos que y = ln (x) es equivalente a e ^ y = x.
y = ln (x) es equivalente a e ^ y = x
De acuerdo, solo unos pocos pasos más, ¡y tendremos nuestra fórmula! Lo siguiente que queremos hacer es tratar y como una función de x, y tomar la derivada de cada lado de la ecuación con respecto a x. Usamos la regla de la cadena en el lado izquierdo de la ecuación para encontrar la derivada. los cadena de reglas es una regla que usamos para tomar la derivada de una composición de funciones y tiene dos formas.
fórmula de la regla de la cadena
El lado izquierdo de la ecuación es e ^ y, donde y es una función de x, por lo que si dejamos f (x) = e ^ x y g (x) = y, entonces f (g (x)) = e ^ y. Dado que la derivada de e a una variable (como e ^ x) es la misma que la original, la derivada de f ‘(g (x)) es e ^ y. Por lo tanto, según la regla de la cadena, la derivada de e y es e ^ y dy / dx. En el lado derecho tenemos la derivada de x, que es 1.
Tenemos (e ^ y) dy / dx = 1. Ahora, recuerde que e y = x. Usaremos este hecho para reemplazar x en nuestra ecuación para e y.
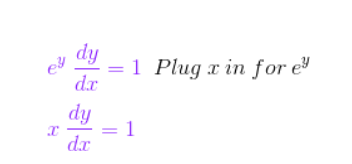pasos para la derivada
Esto nos da la ecuación (x) dy / dx = 1. ¡Ahora nos estamos acercando mucho! ¿Estás tan emocionado como yo? Podemos dividir ambos lados de esta ecuación por x para obtener dy / dx = 1 / x. Lo último es recordar que y = ln (x) y reemplazar esto en nuestra ecuación para y. Tenemos (e ^ y) dy / dx = 1. Ahora, recuerde que e ^ y = x. Usaremos este hecho para reemplazar x en nuestra ecuación para e y.
Derivada ln x
¡Ta-da! Ahora, vemos que d / dx ln (x) = 1 / x, y ahora sabemos por qué esta fórmula para la derivada de ln (x) es verdadera. Entonces, ¿cuál es nuestra solución? La derivada de ln (x) es 1 / x.
Derivada de Ln (x) Resumen
Recuerde los siguientes puntos al encontrar la derivada de ln (x):
- La derivada de ln (x) ln (x) es 1x1x.
- En ciertas situaciones, puede aplicar las leyes de los logaritmos a la función primero y luego tomar la derivada.
- Valores como ln (5) ln (5) y ln (2) ln (2) son constantes; sus derivadas son cero.
ln (x + y) ln (x + y) NO ES IGUAL a ln (x) + ln (y) ln (x) + ln (y); para una función con adición dentro del tronco natural, necesita la regla de la cadena.
ln (x – y) ln (x – y) NO ES IGUAL a ln (x) –ln (y) ln (x) –ln (y); para una función con resta dentro del logaritmo natural, necesita la regla de la cadena.
Derivada de lnx ^ 2
Los pasos para calcular
Veamos nuestro primer método, el cadena de reglas. ¿Cómo funciona la regla de la cadena? Bueno, en primer lugar, la regla de la cadena es una fórmula para calcular la composición de dos o más funciones. Digamos que tenemos una función con un argumento complicado, como sin x2. La función es seno y el argumento es x2. Si el argumento fuera simplemente x, diferenciaríamos sen x y obtendríamos cos x.
Para usar la regla de la cadena, imaginamos que la función tiene un argumento simple y escribimos la derivada. En este ejemplo, la derivada de sen x2 es cos x2. Y luego, multiplicamos por la derivada del argumento. La derivada de x2 es 2x. Por lo tanto, usando la regla de la cadena, la derivada de sen x2 es cos x2 por 2x o solo 2x cos x2.
Paso 1: diferenciar con la regla de la cadena
La derivada de ln x es 1 / x, entonces la derivada de ln x2 es 1 / x2 veces la derivada de x2:
Paso 2: simplificaEntonces, la derivada de x2 es 2x:
1 / x2 por 2x se puede escribir como 2x / x2.
Cancelar el término x común:
Paso 1: reescribe ln x2 usando propiedades de logaritmo
Ahora, veamos nuestro segundo método, el propiedades de los logaritmos, que son básicamente las propiedades o características de los exponentes.
El logaritmo de x elevado a n es igual a n veces el logaritmo de x. Por tanto, ln x2 = 2 ln x.
Paso 2: diferenciar
Dejándonos con la derivada de ln x, que es 1 / x La constante 2 sale de la diferenciación:
El 2 multiplicado por 1 / x se escribe como 2 / x:
Paso 3: simplifica
Por tanto, la derivada de ln x2 es 2 / x. Tenga en cuenta que este resultado concuerda con las gráficas de las rectas tangentes para x tanto positivo como negativo. Para x = 2, la derivada es 2/2 = 1, lo que concuerda con la gráfica. Y para x = -2, la derivada es 2 / (- 2) = -1, que concuerda con la recta tangente con pendiente negativa en x = -2.
Antiderivada de ln x
∫lnxdx = xlnx − x + C
Explicación:
La integral (antiderivada) de lnx es interesante porque el proceso para encontrarla no es el esperado.
Usaremos la integración por partes para encontrar ∫lnxdx:
∫udv = uv − ∫vdu
Donde u y v son funciones de x.
Aquí, dejamos:
u = lnx → dudx = 1x → du = 1xdx y dv = dx → ∫dv = ∫dx → v = x
Haciendo las sustituciones necesarias en la fórmula de integración por partes, tenemos:
∫lnxdx = (lnx) (x) −∫ (x) (1xdx)
→ (lnx) (x) −∫x (1xdx)
= xlnx − ∫1dx
=xlnx − x + C → (¡no olvides la constante de integración!)
Derivada de 1 / lnx
= −1x (lnx) 2
Explicación:
puede hacer esto simplemente como ((lnx) −1) ‘
= – (lnx) −2 (lnx) ‘
= – (lnx) −21x
= −1x (lnx) 2
si quieres jugar con ey logs, supongo que podrías decir eso
1y = lnx
e1y = elnx = x
asi que
(e1y) ‘= 1
y
(e1y) ‘= e1y (1y)’
= e1y⋅− (1y2) y ‘
Entonces −e1y (1y2) y ‘= 1
y ‘= – y2⋅1e1y
= – (1lnx) 2⋅1x
= −1x (lnx) 2
Lo mismo pero un poco más complicado y complicado
Derivada de (lnx) ^ 2
dydx = 2x
Explicación:
Aplicando la regla de la cadena, junto con las derivadas d / dx ln (x) = 1x y ddxx2 = 2x, tenemos
dydx = ddxln (x2)
= 1×2 (ddxx2)
= 1×2 (2x)
= 2x
Derivada de lnx 3
Tengo y ‘= 3x
Explicación:
Podemos utilizar una de las propiedades de los logs que nos permiten escribirlo como:
y = 3ln (x)
Entonces podemos derivar como de costumbre:
y ‘= 3⋅1x
También podemos usar la regla de la cadena para obtener el registro primero tal como está y multiplicar por la derivada del argumento:
y ‘= 1×3⋅3×2 = simplificar:
= 3 veces
¿Cuál es la derivada de un logaritmo natural?
La función exponencial tiene una función inversa, que se llama logaritmo natural y se denota como ln (x).
¿Cuál es la derivada de ln 2 x?
La respuesta es 0. La función, ln 2, es una constante. Si quieres saber la derivada de ln x en x = 2, entonces la respuesta es 1/2, ya que la derivada de f (x) = ln x es f ‘(x) = 1 / x y cuando evalúas eso en x = 2, obtienes f ‘(2} = 1/2.
¿Qué son ln y log?
Por lo general, log (x) significa el logaritmo en base 10; también se puede escribir como log10 (x). ln (x) significa el logaritmo en base e; también se puede escribir como loge (x). ln (x) te dice qué potencia debes aumentar e para obtener el número x.
¿Dónde se define el tronco natural?
Dado como el tronco natural se describe en los libros de matemáticas, hay poco “natural”Sobre esto: es definido como la inversa de un ex, un exponente bastante extraño ya. … En (x) (Logaritmo natural) es el tiempo para alcanzar la cantidad x, asumiendo que crecimos continuamente desde 1.0.
¿Cuál es la derivada de Ln (x)?
La derivada de un logaritmo de una función. La derivada de registros con una base distinta de e. Primero, veamos una gráfica de la función logarítmica con base e, es decir: f (x) = loge (x) (generalmente escrito “ln x”).
Publicaciones relacionadas:
La importancia de una buena educación para los estudiantes de derecho 
Ramas de la ciencia: tipos y más 
Lo que necesita saber para ingresar a las mejores escuelas de posgrado en derecho y negocios 
Encontrar el factor común más alto no es difícil | Una guía paso a paso 
Comprendamos más sobre el costo variable promedio 
Las 10 mejores plataformas educativas en línea 
¿Quiere mejorar la habilidad de escritura? Aquí están las herramientas en línea gratuitas 
Lección sobre la calculadora de valor absoluto y la desigualdad 
4 formas de pagar su licenciatura en línea 
Los 6 errores más comunes que los nuevos tutores están destinados a cometer 
Razonamiento deductivo: definición, ejemplos y más 
Cómo hablar con un niño sobre el contacto inadecuado
