Teorema del resto: definición, ejemplos y más

<p>Teorema del resto: definición, ejemplos y más: A todo el mundo le encanta encontrar un atajo, ya sea que se trate de direcciones de conducción o algún otro tipo de tarea larga. Descubrir una forma más rápida y eficiente de llegar al mismo punto final lo hace sentir bien, ya que lo más probable es que haya ahorrado tiempo, esfuerzo y / o dinero. Las matemáticas están llenas de este tipo de atajos y uno de los más útiles es el teorema del resto.

El teorema del resto chino es un teorema que da una solución única a las congruencias lineales simultáneas con módulos coprimos. En su forma básica, el teorema del residuo chino determinará un número p que, cuando se divide por algunos divisores dados, deja residuos dados.

Teorema del residuo / Teorema del residuo polinomial

Definición

El teorema del resto establece que cuando un polinomio, f (x), se divide por un polinomio lineal, (x -a), el resto de esa división será equivalente af (a). En otras palabras, si desea evaluar la función f (x) para un número dado, a, puede dividir esa función por x – a y su resto será igual af (a).

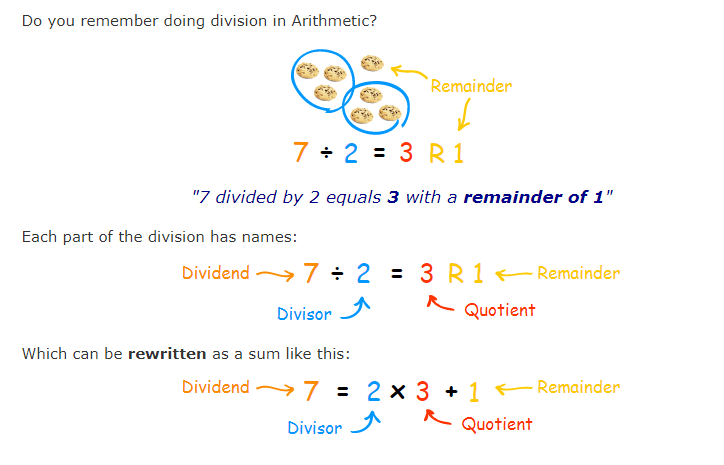
resto básico Cabe señalar que el teorema del resto solo funciona cuando una función se divide por un polinomio lineal, que tiene la forma x + número o x – número. ¿Cómo le ahorra tiempo el teorema del resto? Vamos a averiguar.

Función del teorema del resto

El teorema del resto es especialmente útil cuando se empareja con la división sintética. Si recuerda, una división sintética es un método alternativo para dividir polinomios rápida y fácilmente en lugar de usar una división larga. Además, recuerde que en la división sintética, el número en la fila inferior en la última columna de la derecha es el resto. Por lo tanto, en lugar de insertar un valor y usar un orden de operaciones, puede usar la división sintética como una forma de evaluar un polinomio para un valor dado.

teorema del residuo polinomial

Además, la división sintética y el teorema del resto se pueden usar para determinar si un valor es cero de una función. Con suerte, recuerdas que un cero de una función, por definición, es cualquier punto c, donde f (c) = 0. Por lo tanto, si encuentras un resto de cero después de realizar la división sintética, el número que aparece al principio, denominado a en la definición anterior, se evalúa como cero, o f (a) = 0.

Tenga en cuenta que puede utilizar división larga en lugar de la división sintética, pero casi siempre es más rápido y más fácil usar la división sintética.

Cómo utilizar el teorema

Tomemos la función f (x) = x ^ 4 + 3x ^ 3 – 6x ^ 2 – 6x + 8. Suponga que le dicen que la evalúe para x = 3. Podría dedicar tiempo a introducir un 3 por cada x (los cuatro) enumerados anteriormente. Entonces podría realizar el orden de las operaciones (¿alguien PEMDAS?) Para evaluar los cinco términos. Finalmente, combinaría todos los términos semejantes para obtener la respuesta final para f (3).

Pero es mucho más rápido y fácil usar el teorema del resto. Simplemente configure una división sintética donde dividirá x ^ 4 + 3x ^ 3 – 6x ^ 2 – 6x + 8 por x – 3, y tendrá la respuesta en poco tiempo. Recuerde que dividirá entre x – 3 (no x + 3) porque a = 3 en este ejemplo y el teorema del resto se basa en dividir entre x – a (no x + a). Debe obtener 98 como el resto, lo que significa que f (3) = 98. El trabajo se muestra a continuación.

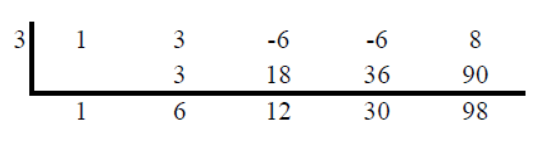método del teorema del resto

Después de realizar la división sintética, debes notar varias cosas. Ahora, evaluemos la misma función para x = -4. Puede usar el mismo proceso de dividir x ^ 4 + 3x ^ 3 – 6x ^ 2 – 6x + 8 por x + 4. Tenga en cuenta que en este ejemplo, dado que a = -4, x – a será x – (- 4) o x + 4.

Teorema del resto chino

En teoría de números, el Teorema del resto chino establece que si se conocen los restos de la división euclidiana de un número entero n entre varios números enteros, entonces se puede determinar de forma única el resto de la división de n entre el producto de estos números enteros, con la condición de que los divisores sean coprimos por pares. La declaración más antigua conocida del teorema es del matemático chino Sunzi en Sunzi Suanjing en el siglo III d.C.

El teorema del resto chino se usa ampliamente para calcular con números enteros grandes, ya que permite reemplazar un cálculo para el cual se conoce un límite en el tamaño del resultado por varios cálculos similares en números enteros pequeños. El teorema del resto chino (expresado en términos de congruencias) es verdadero en todos los dominios ideales principales. Se ha generalizado a cualquier anillo conmutativo, con una formulación que implica ideales.

Sean n1,…, nk números enteros mayores que 1, que a menudo se denominan módulos o divisores. Denotemos por N el producto de ni.

El teorema del resto chino afirma que si los ni son coprimos por pares, y si a1,…, ak son enteros tales que 0 ≤ ai

Esto se puede reformular de la siguiente manera en términos de congruencias: si los ni son coprimos por pares, y si a1, …, ak son números enteros, entonces existe un número entero x tal que

y dos cualesquiera de x es congruente módulo N.

En álgebra abstracta, el teorema a menudo se replantea como: si los ni son coprimos por pares, el mapa

define un isomorfismo de anillo

entre el anillo de números enteros módulo N y el producto directo de los anillos de números enteros módulo ni. Esto significa que para realizar una secuencia de operaciones aritméticas en uno puede hacer el mismo cálculo independientemente en cada y luego obtenga el resultado aplicando el isomorfismo (de derecha a izquierda). Esto puede ser mucho más rápido que el cálculo directo si N y el número de operaciones son grandes. Esto se usa ampliamente, bajo el nombre de computación multimodular, para álgebra lineal sobre los enteros o los números racionales.

El teorema también puede reformularse en el lenguaje de la combinatoria como el hecho de que las progresiones aritméticas infinitas de números enteros forman una familia Helly.

El proceso para resolver sistemas de congruencias con el teorema del resto chino

Para un sistema de congruencias con módulos coprimos, el proceso es el siguiente

Ejemplo de teorema chino del residuo

p1: x = 2 (mod 3)
p2: x = 3 (mod 5)
p3: x = 2 (mod 7)

De p1, x = 3t + 2, para algún número entero t.

Sustituyendo esto en p2 da 3t = 1 (mod 5).

Buscando 1/3 en la tabla de división módulo 5, esto se reduce a una ecuación más simple

p4: t = 2 (mod 5)

que, a su vez, es equivalente a t = 5s + 2 para un entero s.

La sustitución en x = 3t + 2 produce x = 15s + 8.

Esto ahora entra en p3: 15s + 8 = 2 (mod 7).

Lanzar 7 da s = 1 (mod 7). Desde aquí, s = 7u + 1 y,

finalmente, x = 105u + 23.

Tenga en cuenta que 105 = mcm (3,5,7). Así tenemos soluciones 23,128,233,…

¿Cómo se usa el teorema del resto?

En otras palabras, si desea evaluar la función f (x) para un número dado, a, puede dividir esa función por x – a y su recordatorio será igual af (a). Cabe señalar que el teorema del resto sólo funciona cuando una función se divide por un polinomio lineal, que tiene la forma x + número o x – número.

¿Qué es el teorema del resto de la clase 9?

Teorema del resto de polinomios: polinomios, clase 9, matemáticas. TEOREMA DEL RESTO. Si p (x) es cualquier polinomio de grado mayor o igual a 1 y sea a cualquier número real. Cuando p (x) se divide por x– a, entonces el resto es igual ap (a).

¿Cuál es el teorema del factor con el ejemplo?

El resto es cero, por lo que el Teorema del factor dice que: x + 4 es un factor de 5×4 + 16×3 – 15×2 + 8x + 16. En la práctica, el Teorema del factor se usa al factorizar polinomios “completamente”. En lugar de probar varios factores mediante la división larga, utilizará la división sintética y el teorema del factor.

¿Cuál es la fórmula para el resto?

En abstracto, la fórmula clásica del resto es: Dividendo / Divisor = Cociente + Resto / Divisor. Si multiplicamos por el Divisor, obtenemos otra variante útil de la fórmula del resto: Dividendo = Cociente * Divisor + Resto.

¿Qué significa la raíz de una función?

Un número real x se llamará solución o raíz si satisface la ecuación, es decir. Es fácil ver que las raíces son exactamente las intersecciones con el eje x de la función cuadrática, que es la intersección entre la gráfica de la función cuadrática con el eje x. a <0. a> 0.

Mensaje de navegación

Publicaciones relacionadas:

Fórmula de velocidad angular: definición, ejemplo y más Elementos diatómicos: definición, ejemplo y más Propiedad inversa: definición, usos y ejemplos Campo eléctrico entre dos placas: magnitud, dirección, ejemplos y más Elementos principales del caso de lesiones personales Derivada de tangente: pendiente, derivada y más Entropía: definición, fórmula y más Ángulos interiores alternativos: definición, teorema y más El instrumento Mbira: historia, música y tecnología Nueva York del siglo XVII: historia, cronología, mapas y más Razonamiento deductivo: definición, ejemplos y más Fórmula combinada: definición, usos en probabilidad, ejemplos y más