Derivada de tangente: pendiente, derivada y más

<p>Derivada de tangente – La diferenciación de funciones trigonométricas es el proceso matemático de encontrar la derivada de una función trigonométrica, o su tasa de cambio con respecto a una variable. Las funciones trigonométricas comunes incluyen sin (x), cos (x) y tan (x). Por ejemplo, la derivada de f (x) = sin (x) se representa como f ′ (a) = cos (a). f ′ (a) es la tasa de cambio de sen (x) en un punto particular.

Todas las derivadas de funciones trigonométricas circulares se pueden encontrar usando las de sin (x) y cos (x). Luego, se implementa la regla del cociente para diferenciar la expresión resultante. Encontrar las derivadas de las funciones trigonométricas inversas implica el uso de la diferenciación implícita y las derivadas de funciones trigonométricas regulares.

Derivada de tangente

Para encontrar la derivada de una tangente de x, comenzaremos escribiendo tan x como sen x / cos x y luego usaremos la regla del cociente para diferenciar.

derivada de la tangente

los regla del cociente dice que si dos funciones son diferenciables, entonces el cociente también es diferenciable. Aquí está la regla del cociente aplicada a tan x cuando está en forma de sin x / cos x

Derivado

Ahora sabemos que la derivada de sen x es cos x y la derivada de cos x es -sin x. Sustituyendo estas derivadas entre paréntesis y simplificando, obtenemos

Derivado2

Ahora hay dos identidades trigonométricas que podemos usar para simplificar este problema

• sin²x + cos²x = 1
• segundos x = 1 / cos x

Y eso es todo, ¡hemos terminado! La derivada de tan x es sec²x.

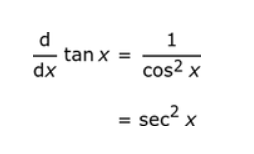La derivada de tan x

Sin embargo, puede haber más para encontrar derivadas de la tangente. En el caso general, tan x es la tangente de una función de x, como tang (x). Tenga en cuenta que en el caso simple, g (x) = x.

Generalmente buscamos

La derivada de tanx

Derivada de la tangente inversa

Las siguientes son las fórmulas para las derivadas de las funciones trigonométricas inversas

Dejamos y = arctan x

Dónde

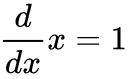Limites

Luego

tan y = x

Usando diferenciación implícita y resolviendo para dy / dx:

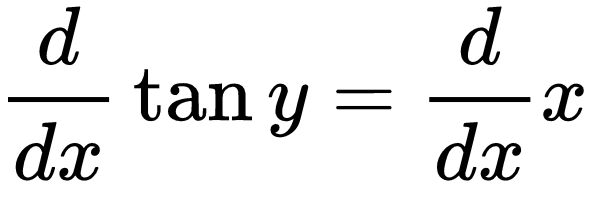derivado de tany

Lado izquierdo

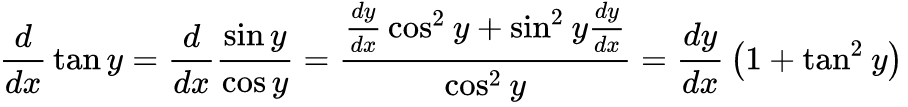Resolver

Lado derecho

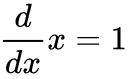Derivada de x

Por lo tanto,

1 + tan2y

Sustituyendo x = tany desde arriba, obtenemos

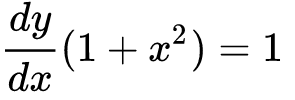derivada de 1 + x2

Pendiente de la derivada de la línea tangente

Rectas tangentes

El primer problema que veremos es el problema de la línea tangente. Antes de entrar en este problema, probablemente sería mejor definir una línea tangente.

Una recta tangente a la función f (x) f (x) en el punto x = ax = a es una recta que toca la gráfica de la función en el punto en cuestión y es “paralela” (de alguna manera) a la gráfico en ese punto. Eche un vistazo al gráfico siguiente.

Pendiente de la derivada de la línea tangente

En este gráfico, la línea es una línea tangente en el punto indicado porque solo toca el gráfico en ese punto y también es “paralela” al gráfico en ese punto. Del mismo modo, en el segundo punto que se muestra, la línea simplemente toca el gráfico en ese punto, pero no es “paralela” al gráfico en ese punto y, por lo tanto, no es una línea tangente al gráfico en ese punto.

En el segundo punto que se muestra (el punto donde la línea no es una línea tangente), a veces llamaremos a la línea Linea secante.

Hemos usado la palabra paralelo un par de veces y probablemente deberíamos tener un poco de cuidado con ella. En general, pensaremos que una línea y un gráfico son paralelos en un punto si ambos se mueven en la misma dirección en ese punto. Entonces, en el primer punto arriba del gráfico y la línea se mueven en la misma dirección, entonces diremos que son paralelas en ese punto. En el segundo punto, por otro lado, la línea y el gráfico no se mueven en la misma dirección, por lo que no son paralelos en ese punto.

Bien, ahora que hemos obtenido la definición de una línea tangente fuera del camino, pasemos al problema de la línea tangente.

¿Cuáles son las derivadas de la tangente?

Derivadas de funciones trigonométricas. Las funciones trigonométricas básicas incluyen las siguientes 6 funciones: seno (Sinx), coseno (Cosx), tangente (Tanx), cotangente (Cotx), secante (Secx) y cosecante (Cscx). Todas estas funciones son continuas y diferenciables en sus dominios.

¿Qué es la derivada de la tangente, una tangente inversa?

La Arctangente de X se define como la función tangente inversa de X cuando X es real (X∈ℝ). Cuando la tangente de Y es igual a X: Tan Y = X. Entonces la Arctangente de X es igual a la función tangente inversa de X, que es igual a Y: Arctan X = Tan-1 X = Y.

¿Cuál es la derivada de Sin2X?

Es decir, Dy / Dx = 2 * Cos (2X). Recuerde que la regla de la cadena establece que uno “diferencia el exterior, deja el interior solo, luego diferencia la función interior”. La derivada de Sin (X) con respecto a X es el Cos (X), y la derivada de 2X con respecto a X es simplemente 2.

¿Qué es una derivada de Cos 2X?

La derivada de Cos (2X) es -2Sin (2X). El proceso de encontrar esta derivada utiliza la regla de la cadena. Podemos utilizar integrales para comprobar nuestro trabajo al encontrar derivadas. Si D (X) es la derivada de F (X), entonces la integral de D (X) es F (X) + C, donde C es una constante.

¿Qué es la fórmula de Sin2X?

Fórmulas de doble ángulo: Sin 2X = 2Sin X Cos X, Cos 2X = Cos2X – Sin2X = 2Cos2X – 1 = 1 – 2Sin2X.

Mensaje de navegación

Publicaciones relacionadas:

Cociente de diferencia: fórmula, calculadora, ejemplos Derivada de sin ^ 2x, sin ^ 2 (2x) y más ¿Cuáles son las obligaciones de un abogado de lesiones personales? Geometría molecular SO2, hibridación, estructura de Lewis y diagrama MO Forma de intersección de pendiente (definición, gráficos y problemas de palabras) Estratificación social: definición, ejemplos y más Países eslavos: los orígenes de las naciones eslavas SOHCAHTOA – Definición y ejemplo Costo de oportunidad: definición, fórmula y ejemplos ¿Qué es un defensor personal y por qué necesita contratar uno? ¿Cómo puede ayudarlo un abogado de lesiones personales? Ácido carboxílico: definición, compuestos y más