La resistencia del transformador se define como la resistencia interna de los devanados primario y secundario. En un transformador real, los devanados primario y secundario tienen cierta resistencia representada por R1 y R2 y las reactancias por X1 y X2. Sea K la relación de transformación.
Para facilitar los cálculos, las resistencias y las reactancias se pueden transferir a cualquier lado, lo que significa que todos los términos primarios se refieren al lado secundario o todos los términos secundarios se refieren al lado primario.
Las caídas resistivas y reactivas en el lado primario y secundario se representan de la siguiente manera
- Caída resistiva en el lado secundario = I2R2
- Caída reactiva en el lado secundario = I2X2
- Caída resistiva en el lado primario = I1R1
- Caída reactiva en el lado primario = I1X1
Lado primario referido al lado secundario
Dado que la relación de transformación es K, la caída resistiva y reactiva primaria referida al lado secundario será K veces, es decir, K I1R1 y K I1X1 respectivamente. Si I1 se sustituye igual a KI2, entonces tenemos una caída resistiva primaria y reactiva referida al lado secundario igual a K2I2R1 y K2I2X1 respectivamente.
La caída resistiva total en un transformador.
La caída reactiva total en un transformador.
Los términos
representan la resistencia y la reactancia equivalentes del transformador referidas al lado secundario.
Donde
Por lo tanto,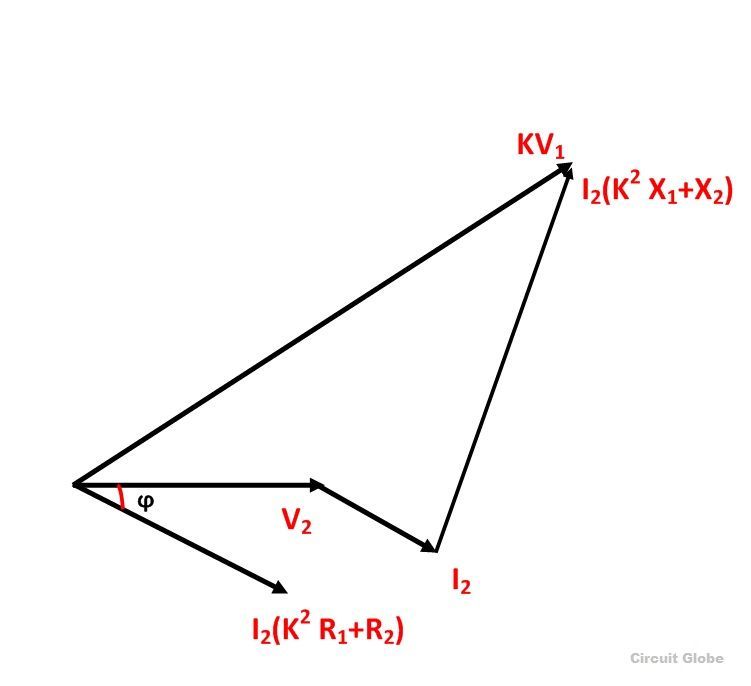
A partir del diagrama fasorial que se muestra arriba, la ecuación se puede formar como
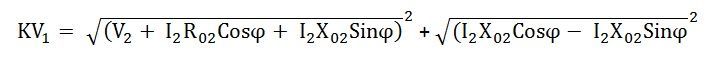Donde V2 es el voltaje del terminal secundario e I2 es la corriente secundaria que va a la zaga del voltaje del terminal V2 en un ángulo ϕ.
Dado que el término
es muy pequeño y se desprecia en comparación con el término 
Ahora la ecuación se convierte en
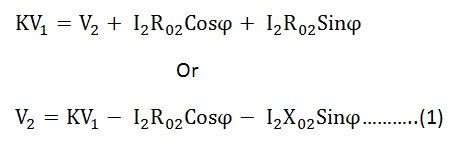
Donde V1 es el voltaje aplicado al devanado primario
Si la carga en el lado secundario del transformador es puramente resistiva, entonces ϕ = 0 y la ecuación (1) se convierte en
Si la carga en el lado secundario del transformador es capacitiva, entonces ϕ debe tomarse como negativo y la ecuación (1) se convierte en
Por lo tanto, este será el voltaje de carga.
Publicaciones relacionadas:
Diferencia entre estator y rotor 
Diferencia entre el filtro FIR y el filtro IIR 
Diferencia entre termopar y termistor 
Tubo de rayos catódicos (CRT) 
Impedancia característica de la línea de transmisión 
Diferencia entre electricidad y magnetismo 
Concepto de estado subtransitorio, transitorio y estacionario 
Construcción de un generador de CC 
Teorema de superposición 
Frenado dinámico y taponamiento 
Cálculo de Componentes Simétricos 
Aislador de suspensión
