<p style=”text-align: justify;”>Tasa instantánea de cambio: Vemos cambios a nuestro alrededor en todas partes. Cuando proyectamos una pelota hacia arriba, su posición cambia con respecto al tiempo y su velocidad cambia a medida que cambia su posición. La altura de una persona cambia con el tiempo. Los precios de las acciones y las opciones cambian con el tiempo. El precio de equilibrio del bien cambia con respecto a la oferta y la demanda. El poder irradiado por un cuerpo negro cambia a medida que cambia su temperatura. El área de la superficie de una esfera cambia a medida que cambia su radio. Esta lista nunca termina. Es sorprendente medir y estudiar estos cambios.
Imagine que conduce a una tienda de comestibles a 10 millas de su casa y le toma 30 minutos llegar allí. Eso significa que viajó 10 millas en 1/2 hora, a una velocidad promedio de 20 millas por hora. (10 millas divididas por 1/2 hora = 20 millas por hora). La velocidad de su automóvil es un gran ejemplo de tasa de cambio.
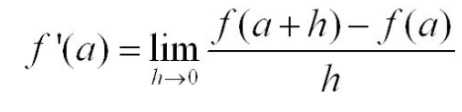
Tasa de cambio promedio e instantánea
Una tasa de cambio le indica qué tan rápido está cambiando algo, como la ubicación de su automóvil mientras conduce. También puede medir qué tan rápido crece su cabello, cuánto dinero gana su negocio cada mes o cuánta agua fluye sobre una presa. Todos estos, y muchos más, se pueden representar calculando la tasa promedio de cambio de una cantidad durante un cierto período de tiempo.
Una forma fácil de calcular una tasa de cambio es hacer un gráfico de la cantidad que cambia en función del tiempo. Luego, puede calcular la tasa de cambio encontrando la pendiente del gráfico, como este. La pendiente se encuentra dividiendo cuánto y los valores cambian por cuánto X los valores cambian. Veamos un gráfico de posición versus tiempo y usémoslo para determinar la tasa de cambio de posición, más comúnmente conocida como velocidad.
Estos cambios dependen de muchos factores; por ejemplo, la potencia irradiada por un cuerpo negro depende de su superficie y de la temperatura. Examinaremos casos en los que solo un factor varía y todos los demás son fijos. Entonces podemos modelar nuestro sistema como y = f (x), y = f (x), donde yy cambia con respecto a xx.
Índice de contenidos
Calculadora de tasa instantánea de cambio
Entonces, vimos que se podía calcular la tasa de cambio promedio calculando la pendiente de una línea, pero ¿funciona eso también para tasas de cambio instantáneas? De hecho, lo hace, aunque tienes que pensar en la pendiente de forma un poco diferente a como lo habías hecho antes.
Si tiene un gráfico de su posición frente al tiempo que NO es una línea recta y desea calcular su velocidad instantánea, puede dibujar una línea, conocida como linea tangente, que solo toca el gráfico en un punto. La pendiente de esta recta tangente le dará la tasa de cambio instantánea exactamente en ese punto.
 |
Como puede ver en el cálculo de este gráfico, v es igual a 20 metros divididos por 5 segundos menos 1,5 segundos, es decir, 3,5 segundos, lo que equivale a 5,7 metros por segundo. ¿Cómo se compara eso con la tasa de cambio promedio? Para determinar su velocidad promedio durante todo el viaje, calcule la pendiente de una línea trazada desde el primer punto en el gráfico hasta el último punto.
Lea también: Cómo calcular la fórmula de velocidad angular
Fórmula de tasa instantánea de cambio
Un automóvil viaja por una carretera recta paralela al eje xx. En t = 0t = 0 segundos, el automóvil está en x = 2x = 2 metros; en t = 6t = 6 segundos, el automóvil está en x = 14x = 14 metros. Encuentre la tasa de cambio promedio de la coordenada xx del automóvil con respecto al tiempo.
Usando la fórmula, obtenemos
text {Rate} = dfrac { Delta x} { Delta t} = dfrac {14 – 2} {6 – 0} = 2 text {m / s}. _ squareRate = ΔtΔx = 6 −014−2 = 2 m / s. □
Cómo encontrar la tasa de cambio instantánea
Retrocedamos un momento y pensemos en ese viaje a la tienda de comestibles nuevamente. Calculamos que su velocidad promedio para todo el viaje fue de 20 millas por hora, pero ¿eso significa que estuvo viajando exactamente a 20 millas por hora durante todo el viaje? ¿Qué pasa cuando lo detuvieron en un semáforo en rojo o se quedó atrapado en un tráfico que no se movía? Durante esos momentos no te movías en absoluto, por lo que tu velocidad era cero.
Cuando mide una tasa de cambio en un instante específico en el tiempo, esto se llama tasa de cambio instantánea. Un tasa promedio de cambio le indica la tasa promedio a la que algo cambió durante un período de tiempo más largo. Mientras se dirigía a la tienda de comestibles, su velocidad cambiaba constantemente. A veces se movía a más de 20 millas por hora y, a veces, más lento. En cada instante en el tiempo, su tasa de cambio instantánea correspondería a su velocidad en ese momento exacto.
Lea también: ¿Qué son los caracteres alfanuméricos?
Cálculo instantáneo de la tasa de cambio
Primero, estos dos problemas nos llevarán al estudio de los límites, que es el tema de este capítulo después de todo. Analizar estos problemas aquí nos permitirá comenzar a comprender qué es un límite y qué nos puede decir acerca de una función.
En segundo lugar, el problema de la tasa de cambio que veremos es uno de los conceptos más importantes que encontraremos en el segundo capítulo de este curso. De hecho, probablemente sea uno de los conceptos más importantes que encontraremos en todo el curso. Entonces, mirarlo ahora hará que comencemos a pensar en él desde el principio. comienzo.
Rectas tangentes
El primer problema que veremos es el problema de la línea tangente. Antes de entrar en este problema, probablemente sería mejor definir una línea tangente.
Una recta tangente a la función f (x) f (x) en el punto x = ax = a es una recta que toca la gráfica de la función en el punto en cuestión y es “paralela” (de alguna manera) a la gráfico en ese punto. Eche un vistazo al gráfico siguiente.
En este gráfico, la línea es una línea tangente en el punto indicado porque solo toca el gráfico en ese punto y también es “paralela” al gráfico en ese punto. Asimismo, en el segundo punto que se muestra, la línea simplemente toca el gráfico en ese punto, pero no es “paralela” al gráfico en ese punto y, por lo tanto, no es una línea tangente al gráfico en ese punto.
En el segundo punto que se muestra (el punto donde la línea no es una línea tangente) a veces llamaremos a la línea Linea secante.
Hemos usado la palabra paralelo un par de veces y probablemente deberíamos tener un poco de cuidado con ella. En general, pensaremos que una línea y un gráfico son paralelos en un punto si ambos se mueven en la misma dirección en ese punto. Entonces, en el primer punto arriba del gráfico y la línea se mueven en la misma dirección, entonces diremos que son paralelas en ese punto. En el segundo punto, por otro lado, la línea y el gráfico no se mueven en la misma dirección, por lo que no son paralelos en ese punto.
Bien, ahora que hemos obtenido la definición de una línea tangente fuera del camino, pasemos al problema de la línea tangente. Probablemente sea mejor hacerlo con un ejemplo.
Lea también: Fórmula del trinomio cuadrado perfecto
Publicaciones relacionadas:
Lección sobre cómo convertir ángulos a radianes 
Ventajas del estudio en línea que debe conocer 
¿Qué es una muerte por negligencia y por qué debería contratar a un abogado? 
Breve sobre la desviación estándar de la distribución de probabilidad 
Algunos detalles importantes sobre la notación de funciones 
La importancia de delinear y preescribir 
Oir conjugación en tiempo pasado 
Elija la opción de escritura: 5 beneficios de contratar servicios de escritura 
Los 7 idiomas más útiles y apropiados para aprender 
Conócete mejor a ti mismo de 7 formas divertidas 
Una cosa o dos sobre 3 4 5 ángulos de triángulo 
Lección sobre tipos de ángulos: descripción general
