Esta publicación mostrará qué significan un nombre de dominio y una serie de una función y cómo calcular las dos cantidades. Antes de involucrarnos en el dominio y rango de una función, expliquemos brevemente qué es un rango.
En matemáticas, puede contrastar una función con una máquina que produce una relación con una entrada ofrecida. Al tomar un ejemplo de equipo de estampación de monedas, podemos ilustrar el significado de una función en función de su cumplimiento.
Cuando inserta una moneda en un dispositivo de marcado, el resultado es un artículo de metal estampado y aplanado. Al considerar un rango, podemos asociar la moneda y el producto de acero aplanado con el dominio y el rango. En este caso, se considera que un rango es el equipo de estampado de monedas.
Al igual que el fabricante de estampado de monedas, que solo puede generar un solo elemento de acero aplanado cada vez, una gama funciona de la misma manera al descomponer un resultado a la vez.
Índice de contenidos
Antecedentes de una función
El concepto de función presentado a principios del siglo XVII cuando René Descartes (1596-1650) utilizó la idea en su libro Geometría (1637) para modelar problemas matemáticos.
Cincuenta años después, luego de la publicación de Geometry, Gottfried Wilhelm Leibniz (1646-1716) presentó el término “rango” Posteriormente, Leonhard Euler (1707-1783) jugó un papel significativo al introducir la estrategia de función idea, y = f (x ).
Aplicación en tiempo real de una función.
Las funciones son muy útiles en matemáticas, ya que nos permiten modelar los problemas de la realidad en un estilo matemático.
A continuación se muestran algunos ejemplos de la aplicación de una función.
Circunferencia de un círculo
El área de un círculo es un rango de su tamaño o radio. puede representar matemáticamente esta afirmación como:
C (d) = d π o C (r) = 2π ⋅ r.
Una sombra
La longitud de la sombra del objeto es un rango de su elevación.
La posición de un objeto que se reubica.
El lugar de un artículo que se reubica, como un automóvil, es un intervalo de tiempo.
Temperatura
El nivel de temperatura de un cuerpo se basa en varias variables e insumos.
Dinero
El interés compuesto o fácil es un rango de tiempo, principal y tasa de interés.
Elevación de objeto
La altura de un objeto es función de su edad y peso corporal.
Habiendo aprendido más sobre un rango, puede proceder a cómo determinar el nombre de dominio y el rango.
¿Qué es el nombre de dominio y el rango de una función?
El dominio de un rango son los números de entrada que, cuando se conectan a un rango, se especifica el resultado. En pocas palabras, podemos determinar el nombre de dominio de un rango como los posibles valores de x que sin duda harán que una fórmula sea precisa.
Algunos de los casos que no harán una función adecuada son cuando una ecuación se divide entre un origen cuadrado absolutamente nulo o desfavorable.
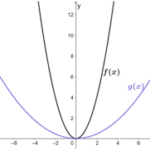
Por ejemplo, f (x) = x2 es un rango legítimo porque, independientemente del valor de x que se pueda reemplazar directamente en la fórmula, siempre hay una respuesta válida. Por lo tanto, podemos concluir que el dominio de cualquier rango son todos los números reales.
El rango de un rango se especifica como una colección de opciones de la ecuación para una entrada determinada. En otras palabras, Range es el resultado del valor y de un rango. Solo hay un rango para un rango proporcionado.
Aprendamos más sobre el rango de una función.
¿Cómo utilizar los símbolos de intervalo para definir el nombre de dominio y el rango?
Dado que la matriz y el dominio de un rango generalmente se revelan en notación de intervalo, es esencial revisar la idea de los símbolos de intervalo.
El procedimiento para hacer símbolos de intervalo consiste en.
Escribe los números divididos por una coma en orden ascendente.
Limite los números utilizando paréntesis () para mostrar que un valor de punto final no está formado por.
Soportes de uso [] para limitar los números cuando el valor de punto final está formado por.
¿Cómo descubrir el dominio y también la serie de una función?
Podemos determinar el dominio de un rango algebraicamente o mediante una técnica visual. Para calcular el nombre de dominio de un rango algebraicamente, se fija la fórmula para calcular los valores de x.
Los diferentes tipos de funciones tienen sus propias técnicas para identificar su dominio.
Veamos estos tipos de rangos y cómo determinar su dominio.
¿Cómo ubicar el nombre de dominio para una función sin denominador ni radicales?
Veamos un par de casos enumerados a continuación para comprender este escenario.
Ejemplo
Descubra el nombre de dominio de f (x) = 5x – 3.
Solución.
Por lo tanto, el nombre de dominio de una función lineal son todos números reales.
Nombre de dominio: (- ∞, ∞).
Rango: (- ∞ ∞).
Una gama con un radical.