Propiedad inversa: En este artículo, comprenderá la definición de propiedad inversa que se aplica a los diferentes tipos de números. También verá ejemplos que le muestran cómo calcular el inverso aditivo y el inverso multiplicativo de un número.
La propiedad inversa de la suma responde que cualquier número sumado a su opuesto será igual a cero. ¿Qué es lo contrario que podrías preguntar? Todo lo que tienes que hacer es cambiar el signo de positivo a negativo o de negativo a positivo. La propiedad inversa de la multiplicación responde que cualquier número multiplicado por su recíproco es igual a 1.
Propiedad inversa
Índice de contenidos
Propiedades de los números reales
Los números reales tienen propiedades únicas, lo que los hace particularmente útiles en la vida cotidiana.
- Los números reales son un conjunto ordenado de números. Esto significa que los números reales son secuenciales. El valor numérico de cada número real encaja entre los valores numéricos de otros dos números reales. Todos se sienten cómodos con este concepto, ya que todas las medidas (peso, poder adquisitivo del dinero, velocidad de un automóvil, etc.) dependen del hecho de que algunos números tienen un valor mayor que otros números. Diez es mayor que cinco y cinco es mayor que cuatro, y así sucesivamente.
- Nunca nos quedamos sin números reales. La variedad de números reales disponibles no es fija. Hay un número infinito de valores disponibles. La disponibilidad de números se expande sin fin. Los números reales no son simplemente una “fila de puntos separados” finita en una recta numérica. Siempre hay otro número real cuyo valor se encuentra entre dos números reales cualesquiera.
- Cuando se suman o multiplican números reales, el resultado es siempre otro número real. (Este no es el caso de todas las operaciones aritméticas. Por ejemplo, la raíz cuadrada de -1 produce un número imaginario).
Con estas tres marcas en mente, la pregunta es:
- ¿Cómo podemos practicar números reales en cálculos prácticos?
- ¿Qué reglas empleamos?
- ¿Cómo se deben sumar, multiplicar, restar y dividir números?
- ¿Qué alcance tenemos?
- ¿Importa lo que hacemos primero? ¿segundo? ¿tercera? ¿cuatro?
- ¿Podemos sumar una racha de números en cualquier orden?
- ¿El resultado será el mismo sin embargo del orden que elijamos?
- ¿Podemos multiplicar una racha de números en cualquier orden?
- ¿Será la respuesta final la misma sin embargo del orden que elijamos?
Las siguientes propiedades de los números reales responden a este tipo de preguntas. Las características de propiedad que siguen muestran cuánta latitud tiene para cambiar la mecánica de los cálculos que utilizan números reales sin cambiar los resultados.
- Propiedad asociativa
- Propiedad conmutativa
- Propiedad distributiva
- Propiedad de identidad
- Propiedad inversa
Propiedad inversa
Definición
Las propiedades inversas se deshacen entre sí. El objetivo de la propiedad inversa de la suma es obtener un resultado de cero. El objetivo de la propiedad inversa de la multiplicación es obtener un resultado de 1. Usamos propiedades inversas para resolver ecuaciones.
En otras palabras, podemos decir que
Una propiedad inversa son dos propiedades que se deshacen entre sí, por ejemplo, suma y resta o multiplicación y división. Puede realizar la misma propiedad inversa en cada lado de una ecuación equivalente sin cambiar la igualdad.
Para cada número real distinto de cero, la propiedad inversa es otro número (llamado número inverso). Una propiedad inversa no es un procedimiento. (La Operación Inversa [explained in the below section] es un procedimiento.)
Todo el conjunto de números reales distintos de cero tiene la propiedad inversa en la suma y la multiplicación porque cada elemento del conjunto tiene una inversa.
Propiedad inversa de la suma
El inverso aditivo de cualquier número es el mismo número con el signo opuesto. Cuando se suman un número y su inverso aditivo, el resultado siempre es 0 (cero) – el elemento de identidad para la adición.
El inverso aditivo de +16 es -16.
Cuando se suman estas dos inversas aditivas:
16 + (-16) = 0
El inverso aditivo de -56 es +56.
Cuando se suman estas dos inversas aditivas:
-56 + 56 = 0
Nota: El inverso aditivo de + A es -A.
Cuando se suman estas dos inversas aditivas:
+ A + (-A) = 0
Propiedad inversa para la multiplicación
El inverso multiplicativo de cualquier número es el recíproco de ese número. Cuando un número y su inverso multiplicativo se multiplican entre sí, el resultado es siempre 1 (uno), el elemento de identidad para la multiplicación.
El inverso multiplicativo de 16 es (1/16).
Cuando estas dos inversas multiplicativas se multiplican entre sí:
16 • (1/16) = (16/1) / (1/16) = 1
El inverso multiplicativo de -56 es 1 / (- 56).
Cuando estas dos inversas multiplicativas se multiplican entre sí:
-56 • (1 / -56) = (-56/1) / (1 / -56) = 1
Nota: El inverso multiplicativo de A es (1 / A)
Cuando estas dos inversas multiplicativas se multiplican entre sí:
A • (1 / A) = (A / 1) / (1 / A) = 1
Las propiedades inversas son claves importantes que se pueden usar para simplificar ecuaciones.
Ejemplos de
Ejemplos de propiedades inversas
Ejemplo 1: Usar la propiedad inversa aditiva
Solución para x
X + 3 = 5
Para eliminar el +3, se puede aplicar la propiedad inversa aditiva de -3 porque +3 – 3 = 0 (el número de identidad aditivo).
Suma el inverso aditivo de -3 a cada lado de la ecuación.
Propiedad inversa aditiva
Ejemplo 2: Uso de la propiedad inversa multiplicativa
Solución para x
2X = 6
Para eliminar el +2 (del 2X), se puede usar la propiedad inversa multiplicativa (del número 2) de ½ porque (2) * (½) = 1 (el elemento de identidad multiplicativo).
Multiplica cada lado de la ecuación por el inverso multiplicativo de ½.
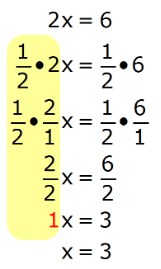Propiedad inversa multiplicativa
Publicaciones relacionadas:
Cociente de diferencia: fórmula, calculadora, ejemplos 
Derivada de sin ^ 2x, sin ^ 2 (2x) y más 
¿Cuáles son las obligaciones de un abogado de lesiones personales? 
Geometría molecular SO2, hibridación, estructura de Lewis y diagrama MO 
Regla de producto y cociente: fórmula y ejemplos 
Forma de intersección de pendiente (definición, gráficos y problemas de palabras) 
Estratificación social: definición, ejemplos y más 
Países eslavos: los orígenes de las naciones eslavas 
Costo de oportunidad: definición, fórmula y ejemplos 
¿Qué es un defensor personal y por qué necesita contratar uno? 
¿Cómo puede ayudarlo un abogado de lesiones personales? 
Ácido carboxílico: definición, compuestos y más
