Tasa de cambio instantánea: fórmula, ejemplo y más

Tasa instantánea de cambio – Una tasa de cambio le indica qué tan rápido está cambiando algo, como la ubicación de su automóvil mientras conduce. También puede medir qué tan rápido crece su cabello, cuánto dinero gana su negocio cada mes o cuánta agua fluye sobre una presa. Todos estos y muchos más se pueden representar calculando la tasa promedio de cambio de una cantidad durante un cierto período de tiempo.

Una forma sencilla de calcular la tasa de cambio es hacer un gráfico de la cantidad que cambia en función del tiempo. Luego, puede calcular la tasa de cambio encontrando la pendiente del gráfico, como este. La pendiente se calcula dividiendo cuánto cambian los valores por cuánto cambian los valores de x. Veamos un gráfico de posición versus tiempo y usémoslo para determinar la tasa de cambio de posición, más comúnmente conocida como velocidad.

Índice de contenidos

Tasa instantánea de cambio
Mensaje de navegación

Tasa instantánea de cambio

Vemos cambios a nuestro alrededor en todas partes. Cuando proyectamos una pelota hacia arriba, su posición cambia con respecto al tiempo y su velocidad cambia a medida que cambia su posición. La altura de una persona cambia con el tiempo. Los precios de las acciones y las opciones cambian con el tiempo. El precio de equilibrio del bien cambia con respecto a la oferta y la demanda. El poder irradiado por un cuerpo negro cambia a medida que cambia su temperatura. El área de la superficie de una esfera cambia a medida que cambia su radio. Esta lista nunca termina. Es sorprendente medir y estudiar estos cambios.

Tasa instantánea de cambio

Estos cambios dependen de muchos factores, por ejemplo, la potencia irradiada por un cuerpo negro depende de su superficie y de la temperatura. Examinaremos casos en los que solo un factor varía y todos los demás son fijos. Entonces podemos modelar nuestro sistema como y = f (x), y = f (x), donde yy cambia con respecto a xx.

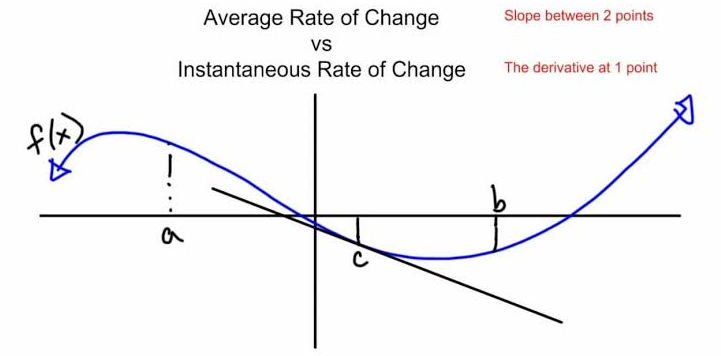
En este gráfico, puede ver cómo la función azul puede tener su tasa de cambio instantánea representada por una línea roja tangente a la curva. Para encontrar la pendiente de esta línea, primero debes encontrar la derivada de la función.

Ejemplo: 2x² + 4, (1,6)

Usando la regla de la potencia para derivadas, terminamos con 4x como derivada. Conectando el valor x de nuestro punto, tenemos

4 (1) = 4

Esto nos dice que la pendiente de nuestra función original en (1,6) es 4, que también representa la tasa de cambio instantánea en ese punto.

Si también quisiéramos encontrar la ecuación de la línea que es tangente a la curva en el punto, que es necesaria para ciertas aplicaciones de derivadas, podemos usar la Forma Punto-Pendiente

y − y1 = m (x − x1)

con m = pendiente de la recta.

Reemplazando nuestro valor de x, y y pendiente, tenemos

y − 6 = 4 (x − 1)

Lo que simplifica a

y = 4x + 2

Los problemas que involucran la tasa instantánea de cambio de una función requieren que use la derivada, aunque podría disfrazarse de una manera con la que no esté familiarizado, como la velocidad de un objeto después de un cierto período de tiempo. Practicar problemas de tasa de cambio similar le ayudará a familiarizarse con los usos prácticos de las derivadas.

Fórmula de tasa instantánea de cambio

La tasa de cambio en un instante conocido es la tasa de cambio instantánea y es equivalente al valor de la derivada en ese punto específico. Entonces se puede decir que, en una función, la pendiente, m de la tangente es equivalente a la tasa de cambio instantánea en un punto específico. Un método más para comprender claramente este concepto es con el cociente de diferencias y los límites. La tasa de cambio promedio de y con respecto ax es el cociente de diferencias. Ahora bien, si uno mira el cociente de diferencias y deja Delta x-> 0, esta será la tasa de cambio instantánea. En palabras sinceras, el intervalo de tiempo es cada vez menor.

La Fórmula de Tasa Instantánea de Cambio provista con límite existe en,

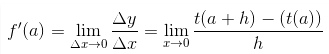Fórmula de tasa instantánea de cambio

Cuando y = f (x), con respecto a x, cuando x = a.

¿Es la derivada la tasa de cambio instantánea?

La derivada como una tasa de cambio instantánea. La derivada nos dice la tasa de cambio de una cantidad en comparación con otra en un instante o punto particular (por eso la llamamos “tasa de cambio instantánea”).

¿Es la velocidad instantánea lo mismo que la tasa de cambio instantánea?

La velocidad es un tipo de tasa de cambio. Es la tasa de cambio de posición con respecto al tiempo. La tasa de cambio es más general e incluye la velocidad como un ejemplo. La palabra “instantáneo” no altera nada de esto.

¿Es la tasa de cambio instantánea un límite?

Tu respuesta final es correcta, muy bien hecha.

La tasa de cambio instantánea, es decir, la derivada, se expresa utilizando un límite. Necesita la notación límite a la izquierda de todas sus expresiones, es decir, la tasa de cambio instantánea de una función f (x) en x = a viene dada simplemente por su derivada en x = a, es decir, f ′ (a).

¿Para qué se utiliza el cambio instantáneo?

Cuando mide una tasa de cambio en un instante específico en el tiempo, esto se denomina tasa de cambio instantánea. Una tasa de cambio promedio le indica la tasa promedio a la que algo cambió durante un período de tiempo más largo.

¿Cuál es la fórmula de la velocidad instantánea?

Usando el cálculo, es posible calcular la velocidad de un objeto en cualquier momento a lo largo de su trayectoria. Esto se llama velocidad instantánea y se define mediante la ecuación v = (ds) / (dt) o, en otras palabras, la derivada de la ecuación de velocidad promedio del objeto.